题目内容
已知:如图,在菱形ABCD中,E、F分别是BC、CD的中点.
(1)求证:△ABE≌△ADF;

(2)过点C作CG∥EA交AF于H,交AD于G,若∠BAE=25°,∠BCD=130°,求∠AHC的度数.
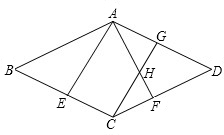
(1)求证:△ABE≌△ADF;

(2)过点C作CG∥EA交AF于H,交AD于G,若∠BAE=25°,∠BCD=130°,求∠AHC的度数.

(1)证明:菱形ABCD中,AB=BC=CD=AD,∠B=∠D,
∵E、F分别是BC、CD的中点,
∴BE=DF.
在△ABE和△ADF中AB=AD,∠B=∠D,BE=DF,
∴△ABE≌△ADF(SAS).(6分)
(2)菱形ABCD中∠BAD=∠BCD=130°,
由(1)得△ABE≌△ADF,
∴∠BAE=∠DAF=25°.
∴∠EAF=∠BAD-∠BAE-∠DAF
=130°-25°-25°=80°.(9分)
又∵AE∥CG,
∴∠EAH+∠AHC=180°.
∴∠AHC=180°-∠EAH=180°-80°=100°.
∴∠AHC=100°.(12分)
∵E、F分别是BC、CD的中点,
∴BE=DF.
在△ABE和△ADF中AB=AD,∠B=∠D,BE=DF,
∴△ABE≌△ADF(SAS).(6分)
(2)菱形ABCD中∠BAD=∠BCD=130°,
由(1)得△ABE≌△ADF,
∴∠BAE=∠DAF=25°.
∴∠EAF=∠BAD-∠BAE-∠DAF
=130°-25°-25°=80°.(9分)
又∵AE∥CG,
∴∠EAH+∠AHC=180°.
∴∠AHC=180°-∠EAH=180°-80°=100°.
∴∠AHC=100°.(12分)

练习册系列答案
相关题目


 E、F.
E、F.
