题目内容
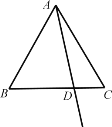
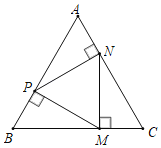
【题目】如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB于点P,MN⊥BC于点M,PN⊥AC于点N.
(1)求证:△PMN是等边三角形;
(2)若AB=18cm,求CM的长.
【答案】(1)证明见解析;(2)6
【解析】
(1)根据等边三角形的性质得出∠A=∠B=∠C,进而得出∠MPB=∠NMC=∠PNA=90°,再根据平角的意义即可得出∠NPM=∠PMN=∠MNP,即可证得△PMN是等边三角形;
(2)易证得△PBM≌△MCN≌△NAP,得出PA=BM=CN,PB=MC=AN,从而求得BM+PB=AB=12cm,根据直角三角形30°角所对的直角边等于斜边的一半得出2PB=BM,即可求得PB的长,进而得出CM的长.
(1)证明:∵△ABC是正三角形,
∴∠A=∠B=∠C,
∵MP⊥AB,MN⊥BC,PN⊥AC,
∴∠MPB=∠NMC=∠PNA=90°,
∴∠PMB=∠MNC=∠APN,
∴∠NPM=∠PMN=∠MNP,
∴△PMN是等边三角形;
(2)解:∵△PMN是等边三角形,
∴PM=MN=NP,
在△PBM、△MCN和△NAP中,
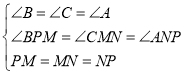 ,
,
∴△PBM≌△MCN≌△NAP(AAS),
∴PA=BM=CN,PB=CM=AN,
∴BM+PB=AB=18cm,
∵△ABC是正三角形,
∴∠A=∠B=∠C=60°,
∴2PB=BM,
∴2PB+PB=18cm,
∴PB=6cm,
∴CM=6cm.

【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?