题目内容
【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2017个小正方形,则需要操作的次数是( )
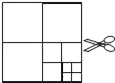
A. 672 B. 671 C. 670 D. 674
【答案】A
【解析】
由题意可知:第一次操作后有正方形4个;第二次操作后正方形的个数为:4﹣1+4=2×4﹣1,第三次操作后正方形的个数有:4﹣1+4﹣1+4=3×4﹣2,第四次操作后正方形的个数有: 4﹣1+4﹣1+4﹣1+4=4×4﹣3,…第n次操作后正方形的个数有:4n﹣(n﹣1)=3n+1,令3n+1=2017,解方程即可求解.
根据题意可得:第n次操作后正方形的个数有(3n+1)个,
设第n次操作后正方形的个数有2017个,
则:3n+1=2017,
解得,n=672,
即:若要得到2017个小正方形,需要操作的次数是672次.
故选A.

练习册系列答案
相关题目
【题目】现从A,B两市场向甲、乙两地运送水果,A,B两个水果市场分别有水果35和15吨,其中甲地需要水果20吨,乙地需要水果30吨,从A到甲地运费50元/吨,到乙地30元/吨;从B到甲地运费60元/吨,到乙地45元/吨
(1)设A市场向甲地运送水果x吨,请完成表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
A市场 | x |
|
B市场 |
|
|
(2)设总运费为W元,请写出W与x的函数关系式,写明x的取值范围;
(3)怎样调运水果才能使运费最少?运费最少是多少元?