题目内容
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2分别交于点C和D,点P在直线l3上.
(1)若点P在C,D两点之间运动,∠PAC,∠APB,∠PBD之间的关系是否发生变化?若变化,请说明理由;若不变,请求出它们之间的关系式.
(2)若点P在C,D两点的外侧运动(点P与点C,D不重合),则∠PAC,∠APB,∠PBD之间的关系又如何?

【答案】(1)∠APB=∠PAC+∠PBD;(2)∠PBD=∠PAC+∠APB.
【解析】
(1)当P点在C、D之间运动时,首先过点P作PE∥l1,由l1∥l2,可得PE∥l2∥l1,根据两直线平行,内错角相等,即可求得:∠APB=∠PAC+∠PBD;
(2)当点P在C、D两点的外侧运动时,由直线l1∥l2,根据两直线平行,同位角相等与三角形外角的性质,即可求得:∠PBD=∠PAC+∠APB.
(1)不变.当点P在C,D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
如图①,
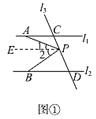
过点P作PE∥l1,
∵l1∥l2,∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD.
(2)如图②,
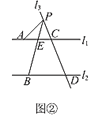
当点P在C,D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD.
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB;
如图③,
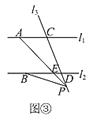
当点P在C,D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC.
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.

【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?



