题目内容
某商场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元。为了扩大销售,增加赢利,商场决定采取适当降价措施。经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。
(1)若该商场平均每天要赢利1200元,且让顾客尽可能感到实惠,每件衬衫应降价多少元?
(2)求该商场平均每天赢利的最大值。
(1)若该商场平均每天要赢利1200元,且让顾客尽可能感到实惠,每件衬衫应降价多少元?
(2)求该商场平均每天赢利的最大值。
(1)20元;(2)1250元
试题分析:(1)设每天利润为w元,每件衬衫降价x元,根据“每件衬衫每降价1元,商场平均每天可多售出2件,商场平均每天要赢利1200元,且让顾客尽可能感到实惠”即可列方程求解;
(2)先配方为顶点式,再根据二次函数的性质求解即可.
(1)设每天利润为w元,每件衬衫降价x元,
根据题意得w=(40-x)(20+2x)=-2x2+60x+800=-2(x-15)2+1250
当w=1200时,-2x2+60x+800=1200,
解之得x1=10,x2=20.
根据题意要尽快减少库存,让顾客得到实惠,所以应降价20元.
答:每件衬衫应降价20元;
(2)商场每天盈利(40-x)(20+2x)=-2(x-15)2+1250.
当x=15元时,商场盈利最多,为1250元
答:每件衬衫降价15元时,商场平均每天盈利最多,为1250元.
点评:一元二次方程的应用是初中数学的重点,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
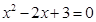 的根的情况是( )
的根的情况是( )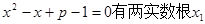 、
、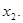
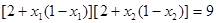 ,求
,求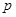 的值.
的值. ,则关于x的一元二次方程
,则关于x的一元二次方程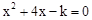 的根的情况是
的根的情况是 是一个完全平方式,则m=_______________。
是一个完全平方式,则m=_______________。
 .
.