题目内容
(2012•海淀区一模)在平面直角坐标系xOy中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…,按如图所示的方式放置、点A1、A2、 A3,…和点B1、B2、B3,…分别在直线y=kx+b和x轴上、已知C1(1,-1),C2(
A3,…和点B1、B2、B3,…分别在直线y=kx+b和x轴上、已知C1(1,-1),C2(
,-
),则点A3的坐标是
 A3,…和点B1、B2、B3,…分别在直线y=kx+b和x轴上、已知C1(1,-1),C2(
A3,…和点B1、B2、B3,…分别在直线y=kx+b和x轴上、已知C1(1,-1),C2(| 7 |
| 2 |
| 3 |
| 2 |
(
,
)
| 29 |
| 4 |
| 9 |
| 4 |
(
,
)
;点An的坐标是| 29 |
| 4 |
| 9 |
| 4 |
(5×(
)n-1-4,(
)n-1)
| 3 |
| 2 |
| 3 |
| 2 |
(5×(
)n-1-4,(
)n-1)
.| 3 |
| 2 |
| 3 |
| 2 |
分析:根据正方形的轴对称性,由C1、C2的坐标可求A1、A2的坐标,将A1、A2的坐标代入y=kx+b中,得到关于k与b的方程组,求出方程组的解得到k与b的值,从而求直线解析式,由正方形的性质求出OB1,OB2的长,设B2G=A3G=b,表示出A3的坐标,代入直线方程中列出关于b的方程,求出方程的解得到b的值,确定出A3的坐标,依此类推寻找规律,即可求出An的坐标.
解答: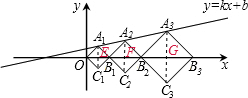
解:连接A1C1,A2C2,A3C3,分别交x轴于点E、F、G,
∵正方形A1B1C1O、A2B2C2B1、A3B3C3B2,
∴A1与C1关于x轴对称,A2与C2关于x轴对称,A3与C3关于x轴对称,
∵C1(1,-1),C2(
,-
),
∴A1(1,1),即(5×(
)1-1-4,(
)1-1),A2(
,
),即(5×(
)2-1-4,(
)2-1),
∴OB1=2OE=2,OB2=OB1+B1F=2+2×(
-2)=5,
将A1与A2的坐标代入y=kx+b中得:
,
解得:
,
∴直线解析式为y=
x+
,
设B2G=A3G=b,则有A3坐标为(5+b,b),
代入直线解析式得:b=
(5+b)+
,
解得:b=
,
∴A3坐标为(
,
),即(5×(
)3-1-4,(
)3-1),
依此类推An(5×(
)n-1-4,(
)n-1).
故答案为:(
,
);(5×(
)n-1-4,(
)n-1).

解:连接A1C1,A2C2,A3C3,分别交x轴于点E、F、G,
∵正方形A1B1C1O、A2B2C2B1、A3B3C3B2,
∴A1与C1关于x轴对称,A2与C2关于x轴对称,A3与C3关于x轴对称,
∵C1(1,-1),C2(
| 7 |
| 2 |
| 3 |
| 2 |
∴A1(1,1),即(5×(
| 3 |
| 2 |
| 3 |
| 2 |
| 7 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴OB1=2OE=2,OB2=OB1+B1F=2+2×(
| 7 |
| 2 |
将A1与A2的坐标代入y=kx+b中得:
|
解得:
|
∴直线解析式为y=
| 1 |
| 5 |
| 4 |
| 5 |
设B2G=A3G=b,则有A3坐标为(5+b,b),
代入直线解析式得:b=
| 1 |
| 5 |
| 4 |
| 5 |
解得:b=
| 9 |
| 4 |
∴A3坐标为(
| 29 |
| 4 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
依此类推An(5×(
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:(
| 29 |
| 4 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
点评:此题考查了一次函数的性质,正方形的性质,利用待定系数法求一次函数解析式,是一道规律型的试题,锻炼了学生归纳总结的能力,灵活运用正方形的性质是解本题的关键.

练习册系列答案
相关题目
 (2012•海淀区一模)如图,在△ABC中,∠C=90°,点D在CB上,DE⊥AB,若DE=2,CA=4,则
(2012•海淀区一模)如图,在△ABC中,∠C=90°,点D在CB上,DE⊥AB,若DE=2,CA=4,则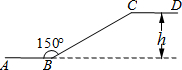 (2012•海淀区一模)如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为
(2012•海淀区一模)如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为