题目内容
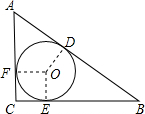已知△ABC三边的长分别为5、12、13，那么△ABC内切圆的半径为________．
2
分析：找到圆与AC、CB、AB的切点，连接OF、OE、OD，得到正方形OFCE，求出CE的长即为圆的半径．
解答：如图，圆O为△ABC内切圆，切点分别为D、E、F，连接OF、OE、OD，则OF⊥AC，OE⊥BC，OD⊥AB．
由切线长定理，可知AF=AD，CF=CE，BD=BE，
∴OE=OF=CE=CF，
又∵52+122=132，∴∠C=90°，
∴四边形FCEO为正方形，
∴CE=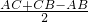
=
=2．
故答案为2．
点评：本题考查了三角形的内切圆与内心、勾股定理的逆定理，构造正方形FCEO是解题的关键．
分析：找到圆与AC、CB、AB的切点，连接OF、OE、OD，得到正方形OFCE，求出CE的长即为圆的半径．
解答：如图，圆O为△ABC内切圆，切点分别为D、E、F，连接OF、OE、OD，则OF⊥AC，OE⊥BC，OD⊥AB．
由切线长定理，可知AF=AD，CF=CE，BD=BE，
∴OE=OF=CE=CF，
又∵52+122=132，∴∠C=90°，
∴四边形FCEO为正方形，
∴CE=
=
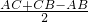
=2．
故答案为2．
点评：本题考查了三角形的内切圆与内心、勾股定理的逆定理，构造正方形FCEO是解题的关键．
练习册系列答案
相关题目
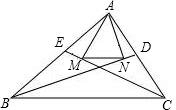如图，自△ABC顶点A向∠C与∠B的角平分线CE、BD作垂线AM、AN，垂足分别是M、N，已知△ABC三边长为a、b、c，则MN=