题目内容
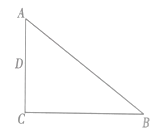
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.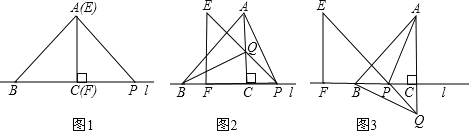
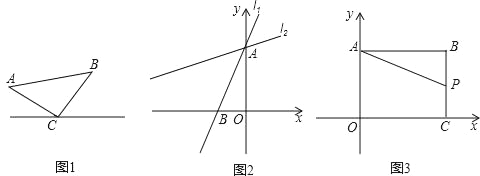
(1)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系,请证明你的猜想;
(2)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系还成立吗?若成立,给出证明;若不成立,请说明理由;
(3)若AC=BC=4,设△EFP平移的距离为x,当0≤x≤8时,△EFP与△ABC重叠部分的面积为S,请写出S与x之间的函数关系式,并求出最大值.
【答案】(1)BQ=AP,证明见解析;(2)BQ=AP,证明见解析;(3)当0≤x<4时,S =-![]() x2+4x;当4≤x≤8时,S=
x2+4x;当4≤x≤8时,S=![]() (8-x)2;当x=
(8-x)2;当x=![]() 时,S的最大值为
时,S的最大值为![]() .
.
【解析】
(1)猜想:BQ=AP.
证明:由题意可知EF⊥FP,又EF=FP,
所以∠EPF=45°,
所以QC=CP,又∠BCQ=∠ACP=90°,AC=BC,
所以△BCQ≌△ACP,
∴BQ=AP;
(2)BQ=AP成立.
证明:∵∠EPF=45°,AC⊥CP,
∴CQ=CP,
又∵BC=AC,
∴Rt△BCQ≌Rt△ACP,
∴BQ=AP;
(3)当0≤x<4时,如图2中,重叠部分是五边形MGFCQ,
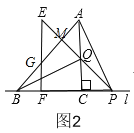
S=S△BMP-2S△BGF=![]() (8-x)2-2×
(8-x)2-2×![]() (4-x)2=-
(4-x)2=-![]() x2+4x,
x2+4x,
当4≤x≤8时,如图3中,重叠部分是△PBG,
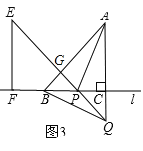
S=S△PBG=![]() (8-x)2,
(8-x)2,
当0≤x<4时,当x=![]() 时,S取最大值为
时,S取最大值为![]() ;
;
当4≤x≤8时,当x=4时,S取最大值为4.
∴当x=![]() 时,S的最大值为
时,S的最大值为![]() .
.

练习册系列答案
相关题目