题目内容
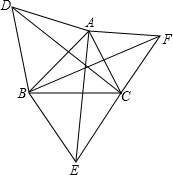
已知：如图分别以△ABC的每一条边，在三角形外作等边三角形，△ABD、△BCE、△ACF，则CD=AE=BF．
正确
分析：已知△ABD、△BCE、△ACF分别是等边三角形，则AD=AB，AC=AF，根据等角的性质可推出∠DAC=∠BAF，从而利用SAS即可判定△ADC≌△ABF，由全等三角形的性质可得CD=BF，同理可证得CD=AE，从而可得CD=AE=BF，故可判定此说法为真．
解答：
证明：AD=AB，
∠DAC=60°+∠BAC=∠BAF，
AC=AF，
∴△ADC≌△ABF（SAS），
∴CD=BF，
同理可证：
CD=AE，
∴CD=AE=BF，
故此说法为真．
点评：此题主要考查学生对全等三角形的判定及性质和等边三角形的性质的理解及运用能力．
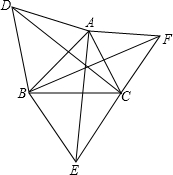
分析：已知△ABD、△BCE、△ACF分别是等边三角形，则AD=AB，AC=AF，根据等角的性质可推出∠DAC=∠BAF，从而利用SAS即可判定△ADC≌△ABF，由全等三角形的性质可得CD=BF，同理可证得CD=AE，从而可得CD=AE=BF，故可判定此说法为真．
解答：
证明：AD=AB，∠DAC=60°+∠BAC=∠BAF，
AC=AF，
∴△ADC≌△ABF（SAS），
∴CD=BF，
同理可证：
CD=AE，
∴CD=AE=BF，
故此说法为真．
点评：此题主要考查学生对全等三角形的判定及性质和等边三角形的性质的理解及运用能力．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
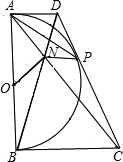已知：如图，以定线段AB为直径作半圆O，P为半圆上任意一点（异于A，B），过点P作半圆O的切线分别交过A，B两点的切线于D，C，AC、BD相交于N点，连接ON、NP．下列结论：①四边形ANPD是梯形；②ON=NP；③DP•PC为定值；④PA为∠NPD的平分线．其中一定成立的是（ ）
14、已知：如图分别以△ABC的每一条边，在三角形外作等边三角形，△ABD、△BCE、△ACF，则CD=AE=BF．（
BC，垂足为F