题目内容
(本小题满分10分)在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为 (0°<
(0°< <180°),得到△A1B1C.
<180°),得到△A1B1C.

(1)如图1,当AB∥CB1时,设A1B1与BC相交于点D.证明:△A1CD是等边三角形;
(2)如图2,连接AA1、BB1,设△ACA1和△BCB1的面积分别为S1、S2.
求证:S1∶S2=1∶3;
(3)如图3,设AC的中点为E,A1B1的中点为P,AC=a,连接EP.当 等于多少度时,EP的长度最大,最大值是多少?
等于多少度时,EP的长度最大,最大值是多少?
【答案】
见解析
【解析】(1)∵AB∥CB′,
∴∠B=∠BC B′=30°,
∴∠A′CD=60°,
又∵∠A′=60∠,
∴∠A′CD=∠A′=∠A′DC=60°,
∴△A′CD是等边三角形;
(2)在Rt△ACB中∠ABC=30°
∴AC:BC=1: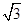
又∵旋转角度为θ
∴∠ACA'=∠BCB'
又∵将△ABC旋转到△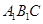
∴AC=A'C CB=CB'
∴AC:BC=A'C:B'C=1: 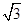
∴△ACA'∽△BCB'
∴S1∶S2=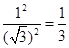
(3)(3)当E,C,P三点在一条直线上时取得最大值,即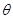 旋转120°,EP=
旋转120°,EP=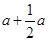 =
= .
.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 .
.



 的值.
的值.