题目内容
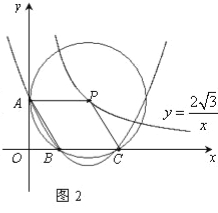
【题目】在直角坐标系![]() 中,已知点P是反比例函数
中,已知点P是反比例函数![]() (
(![]() >0)图象上一个动点,以P为圆心的圆始终与
>0)图象上一个动点,以P为圆心的圆始终与![]() 轴相切,设切点为A.
轴相切,设切点为A.
(1)如图1,⊙P运动到与![]() 轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与![]() 轴相交,设交点为B,C.当四边形ABCP是菱形时:
轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的![]() .若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
.若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.

【答案】(1)、正方形;(2)、①、A(0,![]() ),B(1,0)C(3,0);②、(0,
),B(1,0)C(3,0);②、(0,![]() ),(3,0),(4,
),(3,0),(4,![]() ),(7,8
),(7,8![]() ).
).
【解析】
试题分析:(1)、根据圆与坐标轴相等得出∠PAO=∠OKP=90°,又因为∠AOK=90°则得出四边形OKPA是矩形,根据OA=OK得出正方形;(2)、①、连接PB,设点P的横坐标为x,则纵坐标为![]() ,根据四边形为菱形得出△PBC为正三角形,得出PB=PA=x,PG=
,根据四边形为菱形得出△PBC为正三角形,得出PB=PA=x,PG=![]() ,根据sin∠PBG的值得出x的值,从而得到PG、PA、BC的值,得出A、B、C三点的坐标;②、根据三点坐标求出二次函数的解析式,然后求出直线BP的解析式,列出方程求出点M的坐标.
,根据sin∠PBG的值得出x的值,从而得到PG、PA、BC的值,得出A、B、C三点的坐标;②、根据三点坐标求出二次函数的解析式,然后求出直线BP的解析式,列出方程求出点M的坐标.
试题解析:(1)、四边形OKPA是正方形.
∵⊙P分别与两坐标轴相切,∴PA⊥OA,PK⊥OK.∴∠PAO=∠OKP=90°. 又∵∠AOK=90°,
∴∠PAO=∠OKP=∠AOK=90°.∴四边形OKPA是矩形.又∵OA=OK,∴四边形OKPA是正方形.
(2)、①、连接PB,设点P的横坐标为x,则其纵坐标为![]() .过点P作PG⊥BC于G.
.过点P作PG⊥BC于G.
∵四边形ABCP为菱形,∴BC=PA=PB=PC.∴△PBC为等边三角形.
在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=![]() .sin∠PBG=
.sin∠PBG=![]() ,即
,即![]() .
.
解之得:x=±2(负值舍去).∴PG=![]() ,PA=BC=2.
,PA=BC=2.
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,∴OB=OG﹣BG=1,OC=OG+GC=3.
∴A(0,![]() ),B(1,0)C(3,0).
),B(1,0)C(3,0).
设二次函数解析式为:y=ax2+bx+c.据题意得: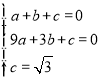
解之得:a=![]() ,b=-
,b=-![]() ,c=
,c=![]() .
.
∴二次函数关系式为:![]() .
.
②、设直线BP的解析式为:y=ux+v,据题意得: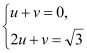
解之得:u=![]() ,v=-3
,v=-3![]() .∴直线BP的解析式为:
.∴直线BP的解析式为:![]() .
.
过点A作直线AM∥PB,则可得直线AM的解析式为:y=![]() x+
x+![]() .
.
解方程组: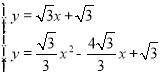 得:
得: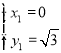 ;
;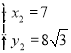 .
.
过点C作直线CM∥PB,则可设直线CM的解析式为:y=![]() x+t.
x+t.
∴0=3![]() +t.∴t=-3
+t.∴t=-3![]() .∴直线CM的解析式为:y=
.∴直线CM的解析式为:y=![]() x-3
x-3![]() .
.
解方程组: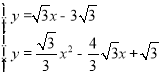 得:
得:![]() ;
;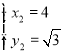 .
.
综上可知,满足条件的M的坐标有四个,
分别为:(0,![]() ),(3,0),(4,
),(3,0),(4,![]() ),(7,8
),(7,8![]() ).
).

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案