��Ŀ����
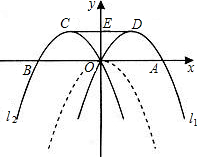
��ͼ����������y=-x2�����߲��֣�����ƽ��1����λ���ȣ�������ƽ��1����λ���ȣ��ó�������l1��������l2��������l1����y��Գƣ���A��O��B�ֱ���������l1��l2��x��Ľ��㣬D��C�ֱ���������l1��l2�Ķ��㣬�߶�CD��y���ڵ�E����1���ֱ�д��������l1��l2�Ľ���ʽ��
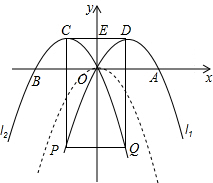
��2����Pʹ������l1����D��O���㲻�غϵ�����һ�㣬Q����P�����y��ĶԳƵ㣬���ж���P��Q��C��DΪ������ı�����ʲô������ı��Σ���˵�����ɣ�
��3����������l1���Ƿ���ڵ�M��ʹ��S��ABM=S�ı���AOED��������ڣ����M�����
 �ꣻ��������ڣ���˵�����ɣ�
�ꣻ��������ڣ���˵�����ɣ�
��������1�����ݶ��κ���ͼ������Ҽ����ϼ��¼�����ƽ�ƹ��ɼ��ɵõ�l1�Ľ���ʽ��
����l1��l2����y��Գƣ������ǵĶ����������y��Գƣ������ڴ�С�����ڷ�����y��Ľ��㶼��ͬ���ݴ˿����l2�Ľ���ʽ��
��2��������ԳƵ����ʣ������ԵĿ��Կ����ı���PQCD�ǵ������Σ���PΪl1�ĶԳ�����������l2�Ľ���ʱ��PQ=CD����ʱ�ı���PQCD�Ǿ��Σ�
��3������������l1�Ľ���ʽ�������A��D��E�����꣬�������������AOED����������ɵõ���ABM�����������AB�Ƕ�������ô���ݡ�ABM������������M��������ľ���ֵ���������������l1�Ľ���ʽ�У��������M������꣮
����l1��l2����y��Գƣ������ǵĶ����������y��Գƣ������ڴ�С�����ڷ�����y��Ľ��㶼��ͬ���ݴ˿����l2�Ľ���ʽ��
��2��������ԳƵ����ʣ������ԵĿ��Կ����ı���PQCD�ǵ������Σ���PΪl1�ĶԳ�����������l2�Ľ���ʱ��PQ=CD����ʱ�ı���PQCD�Ǿ��Σ�
��3������������l1�Ľ���ʽ�������A��D��E�����꣬�������������AOED����������ɵõ���ABM�����������AB�Ƕ�������ô���ݡ�ABM������������M��������ľ���ֵ���������������l1�Ľ���ʽ�У��������M������꣮
��� �⣺��1��l1��y=-��x-1��2+1����y=-x2+2x������1�֣�
�⣺��1��l1��y=-��x-1��2+1����y=-x2+2x������1�֣�
l2��y=-��x+1��2+1����y=-x2-2x������2�֣�
��2����P��Q��C��DΪ������ı���Ϊ���λ�������Σ���3�֣�
���ɣ��ߵ�C���D����P���Q����y��Գƣ�
��CD��PQ��x�ᣮ
�ٵ�P����l2�ĶԳ�����l1�Ľ���ʱ����P��Q������ֱ�Ϊ��-1��-3���ͣ�1��-3��������C��D������ֱ�Ϊ��-1��1���ͣ�1��1����
���ԣ�CD=PQ��CP��CD���ı���CPQD�Ǿ��Σ���4�֣�
�ڵ�P�㲻��l2�ĶԳ�����l1�Ľ���ʱ��������Գ����ʣ�
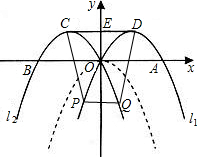 �У�CP=DQ����CQ=DPS������CD��PQ��
��CP=DQ����CQ=DPS������CD��PQ��
���ı���CPQD���ı���CQPD���ǵ������Σ���5�֣�
��3�����ڣ�������������M������Ϊ��x��y��������MA��MB��AD��������ã�
A��2��0����B��-2��0����E��0��1����
S����AOED=
=
����6�֣�
�ٵ�y��0ʱ��S��ABM=
��4��y=
��y=
����7�֣�
��y=
����l1�Ľ���ʽ����ã�x1=
��x2=
��
��M1(
��
)��M2(
��
)����8�֣�
�ڵ�y��0ʱ��S��ABM=
��4��(-y)=
��y=-
����9�֣�
��y=-
����l1�Ľ���ʽ�����x=1��
��
��M3(
��-
)��M4(
��-
)�� ��10�֣�
 �⣺��1��l1��y=-��x-1��2+1����y=-x2+2x������1�֣�
�⣺��1��l1��y=-��x-1��2+1����y=-x2+2x������1�֣�l2��y=-��x+1��2+1����y=-x2-2x������2�֣�
��2����P��Q��C��DΪ������ı���Ϊ���λ�������Σ���3�֣�
���ɣ��ߵ�C���D����P���Q����y��Գƣ�
��CD��PQ��x�ᣮ
�ٵ�P����l2�ĶԳ�����l1�Ľ���ʱ����P��Q������ֱ�Ϊ��-1��-3���ͣ�1��-3��������C��D������ֱ�Ϊ��-1��1���ͣ�1��1����
���ԣ�CD=PQ��CP��CD���ı���CPQD�Ǿ��Σ���4�֣�
�ڵ�P�㲻��l2�ĶԳ�����l1�Ľ���ʱ��������Գ����ʣ�
 �У�CP=DQ����CQ=DPS������CD��PQ��
�У�CP=DQ����CQ=DPS������CD��PQ�����ı���CPQD���ı���CQPD���ǵ������Σ���5�֣�
��3�����ڣ�������������M������Ϊ��x��y��������MA��MB��AD��������ã�
A��2��0����B��-2��0����E��0��1����
S����AOED=
| (1+2)��1 |
| 2 |
| 3 |
| 2 |
�ٵ�y��0ʱ��S��ABM=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
��y=
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
��M1(
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
�ڵ�y��0ʱ��S��ABM=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
��y=-
| 3 |
| 4 |
| ||
| 2 |
��M3(
2+
| ||
| 2 |
| 3 |
| 4 |
2-
| ||
| 2 |
| 3 |
| 4 |
������������Ҫ�����˶��κ���ͼ���ƽ�ơ���ԳƵ����ʡ��������μ����ε��ж���ͼ���������֪ʶ���ۺ�Ӧ��������

��ϰ��ϵ�д�
�����Ŀ
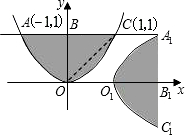 ��ͼ����������y=x2��ֱ��y=1Χ�ɵ�ͼ��OABC��ԭ��O˳ʱ����ת90�������x������ƽ��1����λ�õ�ͼ��O1A1B1C1�������н��۴�����ǣ�������
��ͼ����������y=x2��ֱ��y=1Χ�ɵ�ͼ��OABC��ԭ��O˳ʱ����ת90�������x������ƽ��1����λ�õ�ͼ��O1A1B1C1�������н��۴�����ǣ�������| A����O1�������ǣ�1��0�� | B����C1�������ǣ�2��-1�� | C���ı���OBA1B1�Ǿ��� | D��������OC��������OCA1B1�������3 |
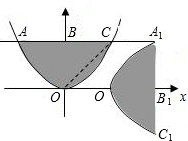 ��ͼ����������y=x2��ֱ��y=1Χ�ɵ�ͼ��OABC��ԭ��O˳ʱ����ת90�������x������ƽ��1����λ�õ�ͼ��O1A1B1C1�������н��۴�����У�����������
��ͼ����������y=x2��ֱ��y=1Χ�ɵ�ͼ��OABC��ԭ��O˳ʱ����ת90�������x������ƽ��1����λ�õ�ͼ��O1A1B1C1�������н��۴�����У����������� ��2012•�㰲����ͼ����������y=
��2012•�㰲����ͼ����������y= ��2012•���֣���ͼ����������y=x2��ֱ��y=xƽ��
��2012•���֣���ͼ����������y=x2��ֱ��y=xƽ��