题目内容
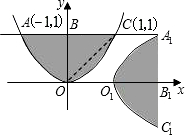 如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,则下列结论错误的是( )
如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,则下列结论错误的是( )| A、点O1的坐标是(1,0) | B、点C1的坐标是(2,-1) | C、四边形OBA1B1是矩形 | D、若连接OC,则梯形OCA1B1的面积是3 |
分析:利用抛物线和平面直角坐标系的性质.
解答:解:根据图形可知:点O的坐标是(0,0),点C的坐标是(1,1).
因为把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,所以点O,C绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到点O1的坐标是(1,0),点C1的坐标是(2,-1),所以选项A,B正确.根据点O(0,0),B(0,1),A1(2,1),B1(2,0)的坐标可得:四边形OBA1B1是矩形,选项C正确.
根据点O(0,0),C(1,1),A1(2,1),B1(2,0)的坐标可得:梯形OCA1B1的面积等于
(1+2)×1=
≠3,所以选项D错误.
故选D.
因为把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,所以点O,C绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到点O1的坐标是(1,0),点C1的坐标是(2,-1),所以选项A,B正确.根据点O(0,0),B(0,1),A1(2,1),B1(2,0)的坐标可得:四边形OBA1B1是矩形,选项C正确.
根据点O(0,0),C(1,1),A1(2,1),B1(2,0)的坐标可得:梯形OCA1B1的面积等于
| 1 |
| 2 |
| 3 |
| 2 |
故选D.
点评:本题难度中等,考查抛物线的旋转、平移及平面直角坐标系的知识.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 标;如果不存在,请说明理由.
标;如果不存在,请说明理由.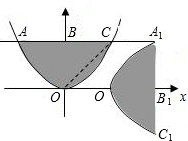 如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,则下列结论错误的有( )个.
如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1,则下列结论错误的有( )个. (2012•广安)如图,把抛物线y=
(2012•广安)如图,把抛物线y= (2012•桂林)如图,把抛物线y=x2沿直线y=x平移
(2012•桂林)如图,把抛物线y=x2沿直线y=x平移