题目内容
如图,已知以Rt△ABC的直角边AB为直径做圆O,与斜边AC交于点D,E为BC边的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)连接OE、AE,当∠CAB为何值时,四边形AODE是平行四边形,并说明理由;
(3)在(2)的条件下,求sin∠CAE的值.
(1)通过证明∠ODE=90°,OD⊥DE,得DE是⊙O的切线 (2) 当∠CAB=45°时,四边形AODE是平行四边形 (3) 
解析试题分析:(1)证明:连接OD、BD.
∵AB是⊙O的直径,∴∠ADB=90°,
∵∠ADB+∠BDC=180°,∴∠BDC=90°,
∵E为BC边的中点,∴BE=DE=CE= BC
BC
∴∠BDE=∠DBE, ∵OB="BD," ∴∠OBD=∠ODB,
又∵∠ABC=∠OBD+∠DBE=90°,
∴∠ODB+∠BDE=90°,即∠ODE=90°,
∴OD⊥DE,∴DE是⊙O的切线. 
(2)解:当∠CAB=45°时,四边形AODE是平行四边形.
又∵∠ABC =90°,∴∠CAB=∠C =45°,∴AB=BC.
同理可得BD="CD," ∵∠BDC=90°,E为BC边的中点,
∴DE⊥BC, ∴∠CED=∠ABC =90°, ∴DE∥AB.
又∵DE= BC,OA=
BC,OA= AB, ∴DE=OA.
AB, ∴DE=OA.
∴四边形AODE是平行四边形.
(3)过点E作EF⊥AC交AC于点F,设EF=x,则CE=BE= x,BC=AB=2
x,BC=AB=2 x,
x,
在Rt△ABE中,AE=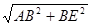 =
= x
x
在Rt△AFE中,sin∠CAE= =
= =
=
考点:直线与圆相切,平行四边形
点评:本题考查直线与圆相切,平行四边形,掌握直线与圆相切的概念和性质,并能判断直线与圆相切,掌握平行四边形的判定方法,会判定一个四边形是平行四边形

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 23、如图,已知以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,
23、如图,已知以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,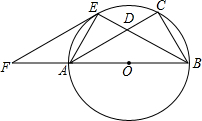 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.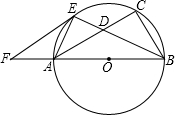 ∥AC交BA的延长线于F.
∥AC交BA的延长线于F.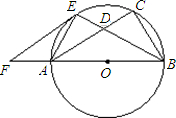 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交