题目内容
当30°<α≤60°时,以下结论正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:分别求出sin30°、sin60°、cos30°、cos60°、tan30°、tan60°、cot30°、cot60°的值即可求出sinα、cosα、tanα、cotα的范围.注意sinα、tanα是增函数,cosα、cotα减函数.
解答:解:A、∵30°<α≤60°,
sin30°=
,sin60°=
,
∴
<sinα≤
,
故此选项正确;
B、∵cos30°=
,cos60°=
,
∴
<cosα≤
:
故此选项错误;
C、∵tan30°=
,tan60°=
,
∴
≤tanα<
,
故此选项错误;
D、∵cot30°=
,cot60°=
,
∴
≤cotα<
,
故此选项错误.
故选A.
sin30°=
| 1 |
| 2 |
| ||
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
故此选项正确;
B、∵cos30°=
| ||
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
故此选项错误;
C、∵tan30°=
| ||
| 3 |
| 3 |
∴
| ||
| 3 |
| 3 |
故此选项错误;
D、∵cot30°=
| 3 |
| ||
| 3 |
∴
| ||
| 3 |
| 3 |
故此选项错误.
故选A.
点评:本题考查的是特殊三角函数值,解决此类题目的关键是熟记特殊角的三角函数.

练习册系列答案
相关题目
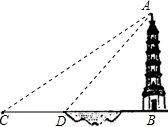 测得A的仰角为β(此时C、D、B三点在同一直线上,小明的身高忽略不计).
测得A的仰角为β(此时C、D、B三点在同一直线上,小明的身高忽略不计). 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米)
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米)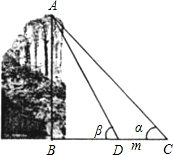 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米)
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米)