题目内容
 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米)
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米)
解:用含α、β和m的式子表示h:
在Rt△ABC中,
∵tanα= ,
,
∴BC= ,
,
在Rt△ABD中,∵tanβ= ,
,
∴BD= ,
,
∵m=BC-BD,
∴m= -
- =
= h-
h- h=50
h=50 -
- =
=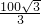 ≈58(m),
≈58(m),
答:h的值是58m.
分析:可分别在Rt△ABC和Rt△ABD中,用AB表示出BC、BD的长,进而由CD=BC-BD=m得到AB即h的表达式,进而代入数据求出即可;
点评:本题考查直角三角形的解法,首先构造直角三角形,再借助角边关系、三角函数的定义解题.
在Rt△ABC中,
∵tanα=
 ,
,∴BC=
 ,
,在Rt△ABD中,∵tanβ=
 ,
,∴BD=
 ,
,∵m=BC-BD,
∴m=
 -
- =
= h-
h- h=50
h=50 -
- =
=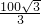 ≈58(m),
≈58(m),答:h的值是58m.
分析:可分别在Rt△ABC和Rt△ABD中,用AB表示出BC、BD的长,进而由CD=BC-BD=m得到AB即h的表达式,进而代入数据求出即可;
点评:本题考查直角三角形的解法,首先构造直角三角形,再借助角边关系、三角函数的定义解题.

练习册系列答案
相关题目
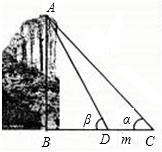 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).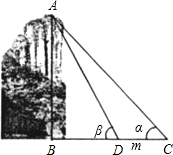 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米)
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米) 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上). ≈1.41,
≈1.41, ≈1.41,
≈1.41, ≈1.73)
≈1.73)