题目内容
当30°<α≤60°时,以下结论正确的是( )
分析:根据锐角三角函数的增减性:当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小),据此即可判断.
解答:解:A、∵sin30°=
,sin60°=
,
∴当30°<α≤60°时,
<sinα≤
,故本选项正确;
B、∵cos30°=
,cos60°=
,
∴当30°<α≤60°时,
≤cosα<
,故本选项错误;
C、∵tan30°=
,tan60°=
,
∴当30°<α≤60°时,
<tanα≤
,故本选项错误;
D、A正确,故本选项错误.
故选A.
| 1 |
| 2 |
| ||
| 2 |
∴当30°<α≤60°时,
| 1 |
| 2 |
| ||
| 2 |
B、∵cos30°=
| ||
| 2 |
| 1 |
| 2 |
∴当30°<α≤60°时,
| 1 |
| 2 |
| ||
| 2 |
C、∵tan30°=
| ||
| 3 |
| 3 |
∴当30°<α≤60°时,
| ||
| 3 |
| 3 |
D、A正确,故本选项错误.
故选A.
点评:本题考查了特殊角的三角函数值及锐角三角函数的增减性,是基础知识,需熟练掌握.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
当30°<α≤60°时,以下结论正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 测得A的仰角为β(此时C、D、B三点在同一直线上,小明的身高忽略不计).
测得A的仰角为β(此时C、D、B三点在同一直线上,小明的身高忽略不计).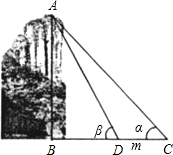 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米)
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米) 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米)
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线 当α=30°,β=60°,m=50米时,求h的值.(精确到1米)