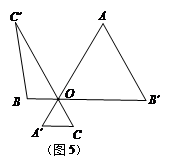题目内容
 (1)如图1,已知平行四边形ABCD中,点E为BC边的中点,延长DE,AB相交于点F.求证:CD=BF.
(1)如图1,已知平行四边形ABCD中,点E为BC边的中点,延长DE,AB相交于点F.求证:CD=BF.(2)如图2,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=
| 3 | 2 |
分析:(1)欲证CD=BF,需证△CDE≌△BFE.由于四边形ABCD是平行四边形,所以DC∥BF,∠1=∠3,∠C=∠2.又点E为BC边的中点,根据AAS,所以△CDE≌△BFE;
(2)由圆周角定理可知∠B=∠D,所以只需在Rt△ACD中,求出∠D的余弦值即可.
(2)由圆周角定理可知∠B=∠D,所以只需在Rt△ACD中,求出∠D的余弦值即可.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,即DC∥AF.
∴∠1=∠F,∠C=∠2.
∵E为BC的中点,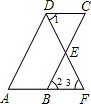
∴CE=BE.
∴△DCE≌△FBE.
∴CD=BF;
(2)解:∵AD是⊙O的直径,r=
,∴∠ACD=90°,AD=3,
∵AC=2,
∴CD=
=
,
∴cosD=
,
∵∠B和∠D是同弧所对的圆周角,
∴∠B=∠D,
∴cosB=cosD=
.
∴DC∥AB,即DC∥AF.
∴∠1=∠F,∠C=∠2.
∵E为BC的中点,

∴CE=BE.
∴△DCE≌△FBE.
∴CD=BF;
(2)解:∵AD是⊙O的直径,r=
| 3 |
| 2 |
∵AC=2,
∴CD=
| 32-22 |
| 5 |
∴cosD=
| ||
| 3 |
∵∠B和∠D是同弧所对的圆周角,
∴∠B=∠D,
∴cosB=cosD=
| ||
| 3 |
点评:(1)本题考查全等三角形的判定和性质,解题的关键是灵活应用平行四边形的各个性质;
(2)此题主要考查的是圆周角定理、勾股定理以及锐角三角函数的定义;能够根据圆周角定理将所求角转化到直角三角形中,是解答此题的关键.
(2)此题主要考查的是圆周角定理、勾股定理以及锐角三角函数的定义;能够根据圆周角定理将所求角转化到直角三角形中,是解答此题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
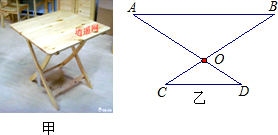 一张折叠型方桌如图甲,其主视图如图乙,已知AO=BO=40cm,C0=D0=30cm,现将桌子放平,两条桌腿叉开的角度∠AOB刚好为120°,则桌面到地面的距离是
一张折叠型方桌如图甲,其主视图如图乙,已知AO=BO=40cm,C0=D0=30cm,现将桌子放平,两条桌腿叉开的角度∠AOB刚好为120°,则桌面到地面的距离是