题目内容
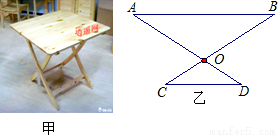
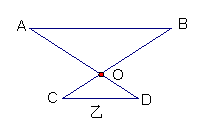
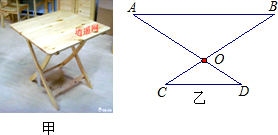 一张折叠型方桌如图甲,其主视图如图乙,已知AO=BO=40cm,C0=D0=30cm,现将桌子放平,两条桌腿叉开的角度∠AOB刚好为120°,则桌面到地面的距离是
一张折叠型方桌如图甲,其主视图如图乙,已知AO=BO=40cm,C0=D0=30cm,现将桌子放平,两条桌腿叉开的角度∠AOB刚好为120°,则桌面到地面的距离是35
35
cm.分析:过点D作DE⊥AB于点E,由等腰三角形的性质得出∠A的度数,再由OA=40cm,OD=30cm求出AD的长度,再根据直角三角形的性质即可求出DE的长.
解答: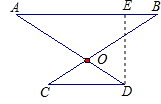 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,
∵AO=BO=40cm,C0=D0=30cm,
∴AD=OA+OD=40+30=70cm,
∵AO=BO,∠AOB=120°,
∴∠A=∠B=
=30°,
∴DE=
AD=
×70=35cm.
故答案为:35.
 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,∵AO=BO=40cm,C0=D0=30cm,
∴AD=OA+OD=40+30=70cm,
∵AO=BO,∠AOB=120°,
∴∠A=∠B=
| 180°-120° |
| 2 |
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:35.
点评:本题考查的是等腰三角形的性质及含30度角的直角三角形,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 一张折叠型方桌如图甲,其主视图如图乙,已知AO=BO=40cm,C0=D0=30cm,现将桌子放平,两条桌腿叉开的角度∠AOB刚好为120°,则桌面到地面的距离是________cm.
一张折叠型方桌如图甲,其主视图如图乙,已知AO=BO=40cm,C0=D0=30cm,现将桌子放平,两条桌腿叉开的角度∠AOB刚好为120°,则桌面到地面的距离是________cm.