Question

【题目】如图，Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D、E，过劣弧 (不包括端点D、E)上任一点作⊙O的切线MN与AB、BC分别交于点M、N.若⊙O的半径为r，则Rt△MBN的周长为( )

A. r B. r C. 2r D. r

Answer 1

【答案】C

【解析】试题解析：

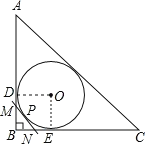
连接OD、OE，

∵O是Rt△ABC的内切圆，

∴OD⊥AB，OE⊥BC，

∵∠ABC=，

∴∠ODB=∠DBE=∠OEB=，

∴四边形ODBE是矩形，

∵OD=OE，

∴矩形ODBE是正方形，

∴BD=BE=OD=OE=r，

∵O切AB于D，切BC于E，切MN于P，NP与NE是从一点出发的圆的两条切线，

∴MP=DM，NP=NE，

∴Rt△MBN的周长为：MB+NB+MN=MB+BN+NE+DM=BD+BE=r+r=2r，

故选C.