题目内容
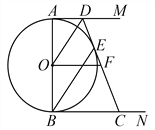
【题目】如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.
(1)求证:OD∥BE;
(2)猜想:OF与CD有何数量关系?并说明理由.
【答案】(1)详见解析;(2)OF=![]() CD,理由详见解析.
CD,理由详见解析.
【解析】试题分析:(1)连接OE,由于AM、DE是![]() 的切线,∠OAD=∠OED=
的切线,∠OAD=∠OED=![]()
那么DA=DE,而OD=OD,于是可证△AOD≌△EOD,从而有![]()
根据圆周角定理有![]() ,那么
,那么![]() 从而有OD∥BE;
从而有OD∥BE;
(2)连接OC,由(1)得∠OCB=∠OCF,而AM∥BN,于是可得![]() 再由(1)得
再由(1)得![]() 易证
易证![]() 从而可知
从而可知![]() 是直角三角形,而F是斜边上的中点,于是
是直角三角形,而F是斜边上的中点,于是![]()
试题解析:(1)证明:连接OE,

∵AM、DE是![]() 的切线,
的切线,
∴DA=DE,∠OAD=∠OED=![]()
又∵OD=OD,
在△AOD和△EOD中,
![]()
∴△AOD≌△EOD,
![]()
![]()
∴∠AOD=∠ABE,
∴OD∥BE;
(2) ![]()
理由:连接OC,
∵BC、CE是O的切线,
∴∠OCB=∠OCF,
∵AM∥BN,
![]()
由(1)得∠ADO=∠EDO,
![]()
即![]()
在Rt△DOC中,
∵F是DC的中点,
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目