Question

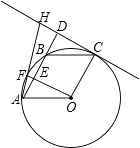
【题目】如图，已知四边形ABCD是矩形，对角线AC的垂直平分线交AD于点E，交BC于点F，连接AF，CE，解答下列问题：
（1）求证：四边形AECF是菱形；
（2）记AB=a，BF=b，若a，b是方程x2﹣2（m+1）x+m2+1=0的两根，问当m为何值时，菱形AECF的周长为8 ．

Answer 1

【答案】
（1）证明：∵四边形ABCD是矩形，

∴AE∥FC，

∴∠EAO=∠FCO，

∵EF垂直平分AC，

∴AO=CO，FE⊥AC，

在△AOE和△COF中， ，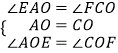

∴△AOE≌△COF（ASA），

∴EO=FO，

∴四边形AFCE为平行四边形，

又∵FE⊥AC，

∴平行四边形AECF为菱形

（2）解：在△ABF中，∵∠ABF=90°，

∴AB2+BF2=AF2，

∴AF2=a2+b2=（a+b）2﹣2ab，

由根与系数的关系得：a+b=2（m+1），ab=m2+1，

∴AF2=[2（m+1）]2﹣2（m2+1）=2m2+8m+2，

∵菱形AECF的周长为8 ，

∴AF=2 ，

∴2m2+8m+2=（2 ）2，

解得：m=1或m=﹣5，

∵原方程有实数根，则△≥0，

∴[﹣2（m+1）]2﹣4（m2+1）≥0，

∴m=﹣5不合题意，舍去，

∴m=1，

即当m=1时，菱形AECF的周长为8

【解析】（1）由ASA证明△AOE≌△COF，得出对应边相等EO=FO，证出四边形AFCE为平行四边形，再由FE⊥AC，即可得出结论．（2）由勾股定理和根与系数的关系得出方程，解方程求出m=1或m=﹣5，再由根的判别式即可得出m的值．
【考点精析】通过灵活运用根与系数的关系和线段垂直平分线的性质，掌握一元二次方程ax2+bx+c=0（a≠0）的根由方程的系数a、b、c而定；两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商；垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题．