题目内容
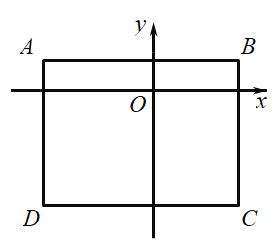
【题目】如图，在平面直角坐标系中，等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系，相似比为1：3，∠ACB＝∠CED＝90°，A、C、E是x轴正半轴上的点，B、D是第一象限的点，BC＝2，则点D的坐标是（ ）
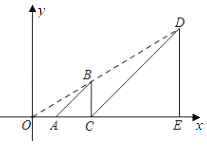
A.（9，6）B.（8，6）C.（6，9）D.（6，8）
【答案】A
【解析】
根据位似变换的定义得到△ACB∽△CED，根据相似三角形的性质求出DE，根据等腰直角三角形的性质求出CE，根据△OCB∽△OED，列出比例式，代入计算即可得到答案．
解：∵等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系，
∴△ACB∽△CED，
∵相似比为1：3，
∴
，即
，
解得，DE＝6，
∵△CED为等腰直角三角形，
∴CE＝DE＝6，
∵BC∥DE，
∴△OCB∽△OED，
∴
，即
，
解得OC＝3，
∴OE＝OC+CE＝3+6＝9，
∴点D的坐标为（9，6），
故选：A．
练习册系列答案
相关题目
【题目】下面是十堰市的三个旅游景点：丹江口的武当山、房县的野人洞、郧西县的五龙河的部分门票价格表．某单位在国庆长假前期给每人购买了一张门票，现将购买门票的情况绘制成如图所示的柱状统计图．
景点 | 标价（元/张） |
武当山 | 200 |
野人洞 |
|
五龙河 | 80 |
请依据上表、图回答下列问题：
（1）去武当山旅游的门票有________张，购买去野人洞旅游的门票占所有门票张数的____________
．
（2）若该单位采取随机抽取的方式把门票分配给员工，在看不到门票的前提下，每人抽取一张（所有门票形状、大小、颜色等完全相同且充分洗匀）．问员工小红抽取去武当山的门票的概率是___________．
（3）若购买去五龙河的总款数占全部款数的
．试求出每张野人洞门票的价格．
