Question

【题目】如图，点D，E分别在等边△ABC的边AB，BC上，将△BDE沿直线DE翻折，使点B落在B1处．若∠ADB1=70°，则∠CEB1=___．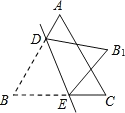

Answer 1

【答案】50°

【解析】

由等边三角形的性质可知：∠B=60°，由邻补角的定义可知∠BDB1=110°，然后由翻折的性质可求得∠BDE=55°，△BDE中由三角形的内角和定理可求得∠BED=65°，然后由翻折的性质可知∠BEB1=130°，从而可求得∠CEB1=50°．

由翻折的性质可知：∠BDE=∠B1DE，
∵∠ADB1=70°，
∴∠BDB1=110°，∴∠BDE=∠BDB1=×110°=55°，
∵△ABC为等边三角形，
∴∠B=60°．
在△BDE中，∠BED=180°-55°-60°=65°．
由翻折的性质可知：∠BEB1=2×65°=130°
∴∠CEB1=180°-130°=50°．
故答案为：50°．