题目内容
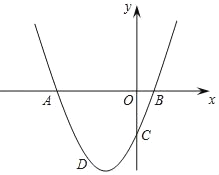
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,3),抛物线顶点为D点.
(1)求此抛物线解析式;
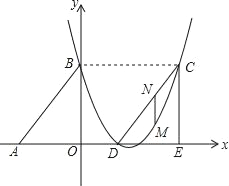
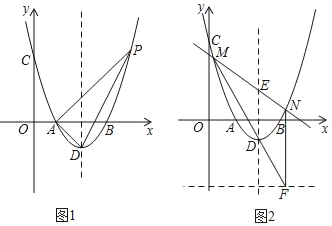
(2)如图1,点P为抛物线上的一个动点,且在对称轴右侧,若△ADP面积为3,求点P的坐标;
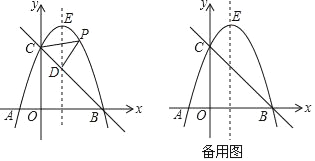
(3)在(2)的条件下,PA交对称轴于点E,如图2,过E点的任一条直线与抛物线交于M,N两点,直线MD交直线y=﹣3于点F,连结NF,求证:NF∥y轴.
【答案】(1)抛物线解析式为:y=x2﹣4x+3;(2)P(4,3);(3)证明见解析.
【解析】
(1)利用待定系数法确定函数关系式;
(2)利用待定系数法求得直线AD的解析式,根据函数图象上点的坐标特征可以设P(t,t2-4t+3),R(t,-t+1).如图1,过点P作PR∥y交AD的延长线于R,由此得到S△ADP=S△APR-S△PDR=![]() PR(t-1)-
PR(t-1)-![]() PR(t-2)=3,PR=6,所以利用关于t的方程求得点P的坐标;
PR(t-2)=3,PR=6,所以利用关于t的方程求得点P的坐标;
(3)欲证明NF∥y轴,只需求得点N、F的横坐标相等即可.
(1)把A(1,0),B(3,0),C(0,3)分别代入y=ax2+bx+c,得
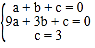 ,
,
解得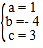 ,
,
所以,该抛物线解析式为:y=x2﹣4x+3;
(2)由(1)知,该抛物线解析式为:y=x2﹣4x+3,
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点D的坐标是(2,﹣1).
如图1,过点P作PR∥y交AD的延长线于R,
由A(1,0),D(2,﹣1)易得直线AD的解析式为:y=﹣x+1.
设P(t,t2﹣4t+3),R(t,﹣t+1).
∴PR=t2﹣3t+2.
∵△ADP面积为3,
∴S△ADP=S△APR﹣S△PDR=![]() PR(t﹣1)﹣
PR(t﹣1)﹣![]() PR(t﹣2)=3,
PR(t﹣2)=3,
∴PR=6,即t2﹣3t+2=6,
解得t1=4,t2=0(舍去).
此时t2﹣4t+3=42﹣4×4+3=3,
∴P(4,3);
(3)证明:∵P(4,3),A(1,0),
∴直线AP为y=x﹣1,
把x=2代入,y=1,
故E(2,1).
设直线MN的解析式为:y=kx﹣2k+1.
联立方程组,得![]() ,
,
消去y,得x2﹣(4+k)x+2+2k=0,
解得x1=![]() ,x2=
,x2=![]() ,
,
∴M(![]() ,
,![]() ),xN=
),xN=![]() .
.
∴直线MN的解析式为y=![]() (x﹣2)﹣1.
(x﹣2)﹣1.
令y=﹣3,得xF=![]() ,
,
即:xN=xF,
∴NF∥y轴.