题目内容
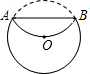 如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O,若⊙O的半径为6cm,则弦AB的长度等于
如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O,若⊙O的半径为6cm,则弦AB的长度等于考点:垂径定理,翻折变换(折叠问题)
专题:计算题
分析:过O作垂直于AB的半径OC,设交点为D,根据折叠的性质可求出OD的长;连接OA,根据勾股定理可求出AD的长,由垂径定理知AB=2AD,即可求出AB的长度.
解答: 解:如图;过O作OC⊥AB于D,交⊙O于C,连接OA,
解:如图;过O作OC⊥AB于D,交⊙O于C,连接OA,
Rt△OAD中,
OD=CD=
OC=3cm,OA=6cm;
根据勾股定理,得:AD=
=3
(cm);
故AB=2AD=6
cm.
故答案为:6
.
 解:如图;过O作OC⊥AB于D,交⊙O于C,连接OA,
解:如图;过O作OC⊥AB于D,交⊙O于C,连接OA,Rt△OAD中,
OD=CD=
| 1 |
| 2 |
根据勾股定理,得:AD=
| OA2-OD2 |
| 3 |
故AB=2AD=6
| 3 |
故答案为:6
| 3 |
点评:此题主要考查了折叠的性质、垂径定理及勾股定理的应用,得出AD的长是解题关键.

练习册系列答案
相关题目
等腰三角形的腰长为4cm,底角为15°,则这个三角形的面积为( )cm2.
| A、无法确定 | B、8 | C、6 | D、4 |
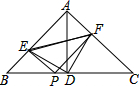 如图,在等腰直角三角形ABC中,AD⊥BC,PE⊥AB,PF⊥AC,则△DEF是
如图,在等腰直角三角形ABC中,AD⊥BC,PE⊥AB,PF⊥AC,则△DEF是