题目内容
等腰三角形的腰长为4cm,底角为15°,则这个三角形的面积为( )cm2.
| A、无法确定 | B、8 | C、6 | D、4 |
考点:等腰三角形的性质,含30度角的直角三角形
专题:计算题
分析:首先根据题意作图,然后过点C作CD⊥AB于D,即可得∠CAD=30°,由直角三角形中,30°角所对的直角边是其斜边的一半,即可求得△ABC的高CD的长,则可求得这个三角形的面积.
解答: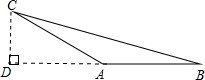 解:如图:AC=AB=4cm,∠B=∠ACB=15°,
解:如图:AC=AB=4cm,∠B=∠ACB=15°,
过点C作CD⊥AB于D,
∴∠CAD=∠ACB+∠B=15°+15°=30°,
∴CD=
AC=2cm(在直角三角形中,30°角所对的直角边是斜边的一半),
∴S△ABC=
AB•CD=
×4×2=4(cm2).
∴这个三角形的面积为4cm2.
故选:D.
 解:如图:AC=AB=4cm,∠B=∠ACB=15°,
解:如图:AC=AB=4cm,∠B=∠ACB=15°,过点C作CD⊥AB于D,
∴∠CAD=∠ACB+∠B=15°+15°=30°,
∴CD=
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴这个三角形的面积为4cm2.
故选:D.
点评:此题考查了含30°角的直角三角形的性质,三角形的外角性质,以及等腰三角形的性质,解题的关键是作出相应的辅助线CD,灵活运用各种性质来解决问题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
对于一次函数y=2x+4,下列结论正确的是( )
| A、函数值随自变量的增大而减小 |
| B、函数的图象不经过第三象限 |
| C、函数的图象向下平移4个单位长度得y=-2x的图象 |
| D、函数的图象与y轴的交点坐标是(0,4) |
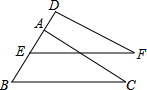 如图,△ABC≌△DEF,BE=4,AE=1,则DA的长是( )
如图,△ABC≌△DEF,BE=4,AE=1,则DA的长是( )| A、5 | B、4 | C、3 | D、2 |
下列方程中解是x=-3的方程是( )
A、
| ||
| B、6x=-2 | ||
C、
| ||
| D、-3x=6 |
以下运算正确的是( )
A、
| ||
| B、2x3+3x2=5x3 | ||
C、
| ||
| D、(-1)2009=-1 |
正方形的面积是4,则它的对角线长是( )
| A、2 | ||
B、
| ||
C、2
| ||
| D、4 |
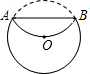 如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O,若⊙O的半径为6cm,则弦AB的长度等于
如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O,若⊙O的半径为6cm,则弦AB的长度等于