题目内容
已知一个一元二次方程的两个根分别是-3和4,试写出满足条件的一个方程: .
考点:根与系数的关系
专题:开放型
分析:先计算-3+4=1,-3×4=-12,然后根据根与系数的关系写出满足条件的一个一元二次方程.
解答:解:∵-3+4=1,-3×4=-12,
∴以-3和4为根的一元二次方程可为x2-x-12=0.
故答案为x2-x-12=0.
∴以-3和4为根的一元二次方程可为x2-x-12=0.
故答案为x2-x-12=0.
点评:本题考查了一元二次方程根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
对于一次函数y=2x+4,下列结论正确的是( )
| A、函数值随自变量的增大而减小 |
| B、函数的图象不经过第三象限 |
| C、函数的图象向下平移4个单位长度得y=-2x的图象 |
| D、函数的图象与y轴的交点坐标是(0,4) |
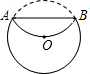 如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O,若⊙O的半径为6cm,则弦AB的长度等于
如图,将⊙O沿着弦AB翻折,劣弧恰好经过圆心O,若⊙O的半径为6cm,则弦AB的长度等于