题目内容
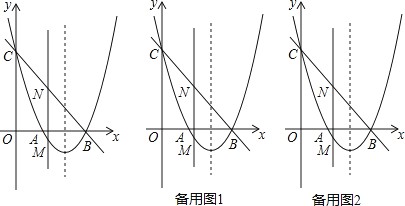
【题目】如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(![]() 4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数y=
4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数y=![]() (k≠0)图象上,当△ADE和△DCO的面积相等时,k的值为( )
(k≠0)图象上,当△ADE和△DCO的面积相等时,k的值为( )
A.-![]()
B.-![]()
C.-3![]()
D.-6![]()
【答案】C
【解析】连接AC,由B的坐标得到等边三角形AOB的边长,得到AO与CO,得到AO=OC,利用等边对等角得到一对角相等,再由∠AOB=60°,得到∠ACO=30°,可得出∠BAC为直角,可得出A的坐标,由三角形ADE与三角形DCO面积相等,且三角形AEC面积等于三角形AED与三角形ADC面积之和,三角形AOC面积等于三角形DCO面积与三角形ADC面积之和,得到三角形AEC与三角形AOC面积相等,进而确定出AE的长,可得出E为AB中点,得出E的坐标,将E坐标代入反比例解析式中求出k的值,即可确定出反比例解析式。
如图,连接AC,
∵点B的坐标为(4,0),△AOB为等边三角形,
∴AO=OB=4.
∴点A的坐标为(2,-2![]() ).
).
∵C(![]() 4,0),∴AO=OC=4,∴∠OCA=∠OAC.
4,0),∴AO=OC=4,∴∠OCA=∠OAC.
∵∠AOB=60°,∴∠ACO=30°.
又∵∠B="60°." ∴∠BAC=90°.
∵S△ADE=S△DCO , S△AEC=S△ADE+S△ADC , S△AOC=S△DCO+S△ADC ,
∴∴S△AEC=S△AOC=![]() ×AEAC=
×AEAC=![]() CO2
CO2![]() , 即
, 即 ![]() AE2
AE2![]() =
=![]() ×2×2
×2×2![]() ,
,
∴E点为AB的中点(3,-![]() ).
).
把E点(3,-![]() )代入y=
)代入y=![]() 中得:k=-3
中得:k=-3![]()
故选C.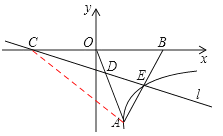
![]()
![]()

练习册系列答案
相关题目