��Ŀ����
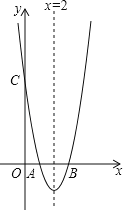
����Ŀ����ͼ1����֪������y����x2+2x+c��x�ύ��A��B���㣬���е�A����1��0������������y�ύ�ڵ�C������ΪD��
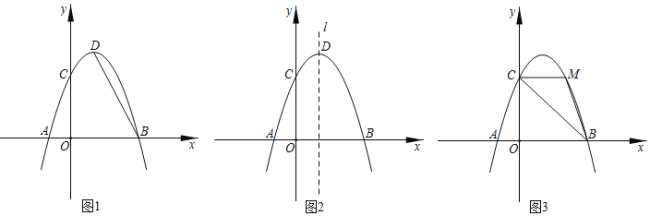
��1����ͼ2��ֱ��l�������ߵĶԳ��ᣬ��P��ֱ��l��һ���㣬�Ƿ���ڵ�P��ʹ��PBC��ֱ�������Σ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
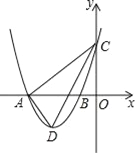
��2����ͼ3������BC����M��ֱ��BC�Ϸ����������ϵ�һ�����㣬����MBC��������ʱ������MBC����������ֵ����N���߶�BC�ϵ�һ�㣬��MN+![]() BN����Сֵ��
BN����Сֵ��
���𰸡���1�����ڣ���P������Ϊ����1��4����1����2����1��![]() ����1��
����1��![]() ������2��
������2��![]()
��������
��1�������ĶԳ���x����![]() ��1�����B��3��0����������⣻
��1�����B��3��0����������⣻
��2����PBΪб�ߡ�PCΪб�ߡ�BCΪб������������ֱ���⼴�ɣ�
��3����MBC�����S��![]() ��MN���OB��
��MN���OB��![]() ����x2+2x+3+x��3����
����x2+2x+3+x��3����![]() ����x2+3x������3x2+
����x2+3x������3x2+![]() x����3��0����S�����ֵΪ
x����3��0����S�����ֵΪ![]() ����ʱ��M��
����ʱ��M��![]() ��
��![]() ����HN����
����HN����![]() BN����MN+
BN����MN+![]() BN��Сֵ��MN��+N��H��MH������N��Ϊ����ĵ�N��������⣮
BN��Сֵ��MN��+N��H��MH������N��Ϊ����ĵ�N��������⣮
��1�������ĶԳ���x����![]() ��1�����B��3��0����
��1�����B��3��0����
�������ߵı���ʽΪ��y������x+1����x��3��������x2��2x��3������x2+2x+3��
���ڣ����ɣ�
�裺��P��1��m����
��PB2��m2+4��PC2����m��3��2+1��BC2��18��
�ٵ�PBΪб��ʱ����m2+4����m��3��2+1+18����ã�m��4��
�ڵ�PCΪб��ʱ��ͬ���ɵã�m����2��
�۵�BCΪб��ʱ��ͬ���ɵã�m��![]() ��
��
�ʵ�P������Ϊ����1��4����1����2����1��![]() ����1��
����1��![]() ����
����
��2������M��MN��x���ڵ�H����BC�ڵ�N����
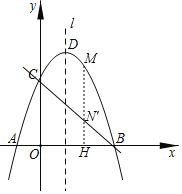
����B��C���������һ�κ�������ʽ����ã�
ֱ��BC�ı���ʽΪ��y����x+3�����CBA��45����
���M��x����x2+2x+3�������N����x����x+3����
��MBC�����S��![]() ��MN���OB��
��MN���OB��![]() ����x2+2x+3+x��3����
����x2+2x+3+x��3����![]() ����x2+3x������3x2+
����x2+3x������3x2+![]() x��
x��
�ߩ�3��0����S�����ֵΪ![]() ����ʱ��M��
����ʱ��M��![]() ��
��![]() ����
����
HN����![]() BN����
BN����
MN+![]() BN��Сֵ��MN��+N��H��MH������N��Ϊ����ĵ�N��
BN��Сֵ��MN��+N��H��MH������N��Ϊ����ĵ�N��
��MN+![]() BN��СֵΪ��MH��yM��
BN��СֵΪ��MH��yM��![]() ��
��

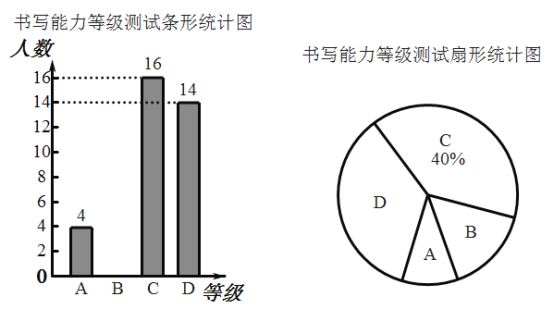
 ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д� A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�