题目内容
 已知抛物线
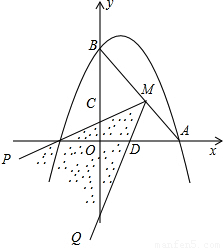
已知抛物线 与x轴和y轴的正半轴分别交于点A和B,已知A点坐标为(4,0).
与x轴和y轴的正半轴分别交于点A和B,已知A点坐标为(4,0).
(1)求抛物线的解析式.
(2)如图,连接AB,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
(3)若抛物线 上有一点F(-k-1,-k2+1),当m,n为何值时,∠PMQ的边过点F?
上有一点F(-k-1,-k2+1),当m,n为何值时,∠PMQ的边过点F?
解:(1)将点A(4,0)代入抛物线解析式可得:0=- ×42+4b+4,
×42+4b+4,
解得:b=1,
故抛物线解析式为y=- x2+x+4;
x2+x+4;
(2)抛物线y=-=- x2+x+4与x轴的交点为A(4,0),与y轴的交点为B(0,4),
x2+x+4与x轴的交点为A(4,0),与y轴的交点为B(0,4),
则AB=4 ,AM=BM=2
,AM=BM=2 ,
,
在∠PMQ绕点M在AB同侧旋转过程中,∠MBC=∠DAM=∠PMQ=45°,
在△BCM中,∠BMC+∠BCM+∠MBC=180°,即∠BMC+∠BCM=135°,
在直线AB上,∠BMC+∠PMQ+∠AMD=180°,即∠BMC+∠AMD=135°,
则∠BCM=∠AMD,
故△BCM∽△AMD,
则 =
= ,即
,即 =
= ,n=
,n= ,
,
故n与m之间的函数关系式为n= (m>0).
(m>0).
(3)∵F(-k-1,-k2+1)在y=- x2+x+4上,
x2+x+4上,
∴- (-k-1)2+(-k-1)+4=-k2+1,
(-k-1)2+(-k-1)+4=-k2+1,
化简得,k2-4k+3=0,
解得:k1=1,k2=3,
即F1(-2,0)或F2(-4,-8),
①MF过点M(2,2)和F1(-2,0),设MF为y=kx+b,
则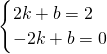 ,
,
解得: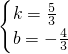 ,
,
故直线MF的解析式为y= x-
x- ,
,
直线MF与x轴的交点为(-2,0),与y轴交点为(0,1),
若MP过点F(-2,0),则n=4-1=3,m= ,
,
若MQ过点F(-2,0),则m=4-(-2)=6,n= ,
,
②MF过点M(2,2)或点F1(-4,-8),设MF为y=kx+b,
则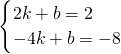 ,
,
解得: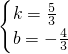 ,
,
故直线MF的解析式为y= x-
x- ,
,
直线MF与x轴的交点为( ,0),与y轴交点为(0,-
,0),与y轴交点为(0,- ),
),
若若MP过点F(-4,-8),则n=4-(- )=
)= ,m=
,m= ,
,
若MQ过点F(-4,-8),则m=4- =
= ,n=
,n= ,
,
故当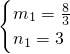 ,
,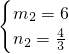 ,
,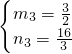 或
或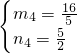 时∠PMQ的边过点F.
时∠PMQ的边过点F.
分析:(1)将点(4,0)代入抛物线解析式可求出b的值,继而得出抛物线的解析式;
(2)先求出AB、BM的长度,通过证明∠BCM=∠AMD,判断△BCM∽△AMD,利用对应边成比例可求出n和m之间的函数关系式;
(3)将点F的坐标代入抛物线解析式求出k的值,分别讨论MP过点F,和MQ过点F的情况,分别得出m、n的值即可.
点评:本题考查了二次函数的综合题,涉及了待定系数法求函数解析式、一次函数图象上点的坐标特征的问题,同学们注意培养自己解决综合题的能力,将所学知识融会贯通.
 ×42+4b+4,
×42+4b+4,解得:b=1,
故抛物线解析式为y=-
 x2+x+4;
x2+x+4;(2)抛物线y=-=-
 x2+x+4与x轴的交点为A(4,0),与y轴的交点为B(0,4),
x2+x+4与x轴的交点为A(4,0),与y轴的交点为B(0,4),则AB=4
 ,AM=BM=2
,AM=BM=2 ,
,在∠PMQ绕点M在AB同侧旋转过程中,∠MBC=∠DAM=∠PMQ=45°,
在△BCM中,∠BMC+∠BCM+∠MBC=180°,即∠BMC+∠BCM=135°,
在直线AB上,∠BMC+∠PMQ+∠AMD=180°,即∠BMC+∠AMD=135°,
则∠BCM=∠AMD,
故△BCM∽△AMD,
则
 =
= ,即
,即 =
= ,n=
,n= ,
,故n与m之间的函数关系式为n=
 (m>0).
(m>0).(3)∵F(-k-1,-k2+1)在y=-
 x2+x+4上,
x2+x+4上,∴-
 (-k-1)2+(-k-1)+4=-k2+1,
(-k-1)2+(-k-1)+4=-k2+1,化简得,k2-4k+3=0,
解得:k1=1,k2=3,
即F1(-2,0)或F2(-4,-8),
①MF过点M(2,2)和F1(-2,0),设MF为y=kx+b,
则
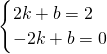 ,
,解得:
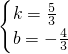 ,
,故直线MF的解析式为y=
 x-
x- ,
,直线MF与x轴的交点为(-2,0),与y轴交点为(0,1),
若MP过点F(-2,0),则n=4-1=3,m=
 ,
,若MQ过点F(-2,0),则m=4-(-2)=6,n=
 ,
,②MF过点M(2,2)或点F1(-4,-8),设MF为y=kx+b,
则
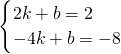 ,
,解得:
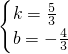 ,
,故直线MF的解析式为y=
 x-
x- ,
,直线MF与x轴的交点为(
 ,0),与y轴交点为(0,-
,0),与y轴交点为(0,- ),
),若若MP过点F(-4,-8),则n=4-(-
 )=
)= ,m=
,m= ,
,若MQ过点F(-4,-8),则m=4-
 =
= ,n=
,n= ,
,故当
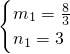 ,
,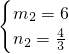 ,
,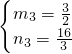 或
或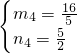 时∠PMQ的边过点F.
时∠PMQ的边过点F.分析:(1)将点(4,0)代入抛物线解析式可求出b的值,继而得出抛物线的解析式;
(2)先求出AB、BM的长度,通过证明∠BCM=∠AMD,判断△BCM∽△AMD,利用对应边成比例可求出n和m之间的函数关系式;
(3)将点F的坐标代入抛物线解析式求出k的值,分别讨论MP过点F,和MQ过点F的情况,分别得出m、n的值即可.
点评:本题考查了二次函数的综合题,涉及了待定系数法求函数解析式、一次函数图象上点的坐标特征的问题,同学们注意培养自己解决综合题的能力,将所学知识融会贯通.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 (2012•岳阳一模)如图,已知抛物线与x轴交于A(-4,0)和B(1,0)两点,与y轴交于C(0,-2)点.
(2012•岳阳一模)如图,已知抛物线与x轴交于A(-4,0)和B(1,0)两点,与y轴交于C(0,-2)点. 与x轴和y轴的正半轴分别交于点A和B,已知A点坐标为(4,0).
与x轴和y轴的正半轴分别交于点A和B,已知A点坐标为(4,0).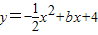 上有一点F(-k-1,-k2+1),当m,n为何值时,∠PMQ的边过点F?
上有一点F(-k-1,-k2+1),当m,n为何值时,∠PMQ的边过点F?