题目内容
【题目】已知△ABC 中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)如图1,连接CE,
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.

【答案】(1)①40°;②30°;(2)50°,130°,10°
【解析】试题分析:(1)①根据三角形的内角和得到∠ABC=80°,由角平分线的定义得到∠ABE=![]() ∠ABC=40°,根据平行线的性质即可得到结论;
∠ABC=40°,根据平行线的性质即可得到结论;
②根据邻补角的定义得到∠ACD=180°-∠ACB=140°,根据角平分线的定义得到∠CBE=![]() ∠ABC=40°,∠ECD=
∠ABC=40°,∠ECD=![]() ∠ACD=70°,根据三角形的外角的性质即可得到结论;
∠ACD=70°,根据三角形的外角的性质即可得到结论;
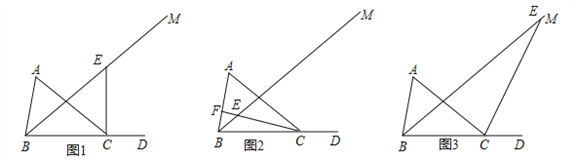
(2)①如图1,当CE⊥BC时,②如图2,当CE⊥AB于F时,③如图3,当CE⊥AC时,根据垂直的定义和三角形的内角和即可得到结论.
试题解析:(1)①∵∠A=60°,∠ACB=40°,
∴∠ABC=80°,
∵BM平分∠ABC,
∴∠ABE=![]() ∠ABC=40°,
∠ABC=40°,
∵CE∥AB,
∴∠BEC=∠ABE=40°;
②∵∠A=60°,∠ACB=40°,
∴∠ABC=80°,∠ACD=180°-∠ACB=140°,
∵BM平分∠ABC,CE平分∠ACD,
∴∠CBE=![]() ∠ABC=40°,∠ECD=
∠ABC=40°,∠ECD=![]() ∠ACD=70°,
∠ACD=70°,
∴∠BEC=∠ECD-∠CBE=30°;
(2)①如图1,当CE⊥BC时,
∵∠CBE=40°,
∴∠BEC=50°;
②如图2,当CE⊥AB于F时,
∵∠ABE=40°,
∴∠BEC=90°+40°=130°,
③如图3,当CE⊥AC时,
∵∠CBE=40°,∠ACB=40°,
∴∠BEC=180°-40°-40°-90°=10°.

练习册系列答案
相关题目



