题目内容
【题目】在面积为60的ABCD中,过点A作AE⊥直线BC于点E,作AF⊥直线CD于点F,若AB=10,BC=12,则CE+CF的值为( )
A.22+11![]()
B.22﹣11![]()
C.22+11![]() 或22﹣11
或22﹣11![]()
D.22+11![]() 或2+
或2+![]()
【答案】D
【解析】解:分两种情况:①如图1所示:∠A为锐角时;
∵平行四边形ABCD的面积=BCAE=ABAF=60,AB=10,BC=12,
∴AE=5,AF=6,
∵AE⊥直线BC于点E,作AF⊥直线CD于F,
∴∠AEB=∠AFD=90°,
∴BE=![]() =5
=5![]() , DF=
, DF=![]() =6
=6![]() ,
,
∴CE=12+5![]() , CF=10+6
, CF=10+6![]() ,
,
∴CE+CF=22+11![]() ;
;
②如图2所示:∠A为钝角时;
由①得:CE=10﹣5![]() , CF=6
, CF=6![]() ﹣10,
﹣10,
∴CE+CF=2+![]() ;
;
故选:D.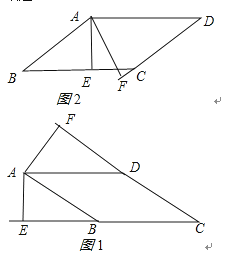
分两种情况:①由平行四边形ABCD的面积求出AE=5,AF=6,再根据勾股定理求出BE、DF,求出CE、CF,即可得出结果;
②CE=10﹣5![]() , CF=6
, CF=6![]() ﹣10,即可得出结果.
﹣10,即可得出结果.

练习册系列答案
相关题目


