题目内容
如图AB为⊙O的直径，C为半圆AB上一点，过C作CD⊥AB交圆于点D，CP平分∠DOC，当C在半圆AB上运动时，则点P
- A.到CD的距离不变
- B.位置不变
- C.等分弧BD
- D.随点C的运动而运动
B
分析：连接OP，通过求证OP⊥AB，即可推出点P的位置不变，根据OC=OP，由角平分线的性质，即可推出OP∥CD，再由CD⊥AB，即可推出OP⊥AB．
解答：连接OP，
∵CP平分∠DOC，
∴∠DCP=∠PCO，
∵OC=OP，
∴∠PCO=∠OPC，
∴∠DCP=∠OPC，
∴OP∥CD，
∵CD⊥AB，
∴OP⊥AB，
∴P点的位置不变．
故选B．
点评：本题主要考查点到直线的距离、垂径定理、平行线的判定及性质、角平分线的性质，关键在于运用数形结合的思想求出PO⊥AB，根据O点为圆心，位置不变，即可推出P点的位置不变．
分析：连接OP，通过求证OP⊥AB，即可推出点P的位置不变，根据OC=OP，由角平分线的性质，即可推出OP∥CD，再由CD⊥AB，即可推出OP⊥AB．
解答：连接OP，
∵CP平分∠DOC，
∴∠DCP=∠PCO，
∵OC=OP，
∴∠PCO=∠OPC，
∴∠DCP=∠OPC，
∴OP∥CD，
∵CD⊥AB，
∴OP⊥AB，
∴P点的位置不变．
故选B．
点评：本题主要考查点到直线的距离、垂径定理、平行线的判定及性质、角平分线的性质，关键在于运用数形结合的思想求出PO⊥AB，根据O点为圆心，位置不变，即可推出P点的位置不变．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
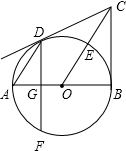如图AB为⊙O的直径，BC⊥AB于点B，连接OC交⊙O于E，弦AD∥OC，弦DF⊥AB于点G．
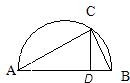9、如图AB为半圆的直径，C为半圆上的一点，CD⊥AB于D，连接AC，BC，则与∠ACD互余的角有（ ）
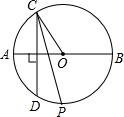如图AB为⊙O的直径，C为半圆AB上一点，过C作CD⊥AB交圆于点D，CP平分∠DOC，当C在半圆AB上运动时，则点P（ ）
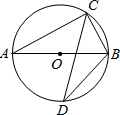如图AB为⊙O的直径，C、D是⊙O上两点，若∠ABC=55°，则∠D的度数为
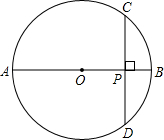如图AB为⊙O的直径，弦AB⊥CD，垂足为P，BP=2，CD=16，求直径AB的长．