题目内容
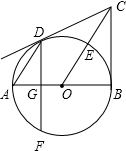如图AB为⊙O的直径，BC⊥AB于点B，连接OC交⊙O于E，弦AD∥OC，弦DF⊥AB于点G．（1）求证：CD为⊙O切线；
（2）若sin∠BAD=
| 4 | 5 |
分析：（1）连接OD，由于AD∥OC，OA=OD=OB，那么∠BOC=∠DAB=∠ADO=∠DOC，而OD=OB，OC=OC，利用SAS可证△ODC≌△OBC，又BC⊥AB，故∠B=90°，所以∠ODC=90°，即CD是⊙O的切线；
（2）在△ADG中SinA=
=
，可先设DG=4x，AD=5x，根据垂径定理可知AB⊥DF，即∠AGD=90°，再利用勾股定理可求AG=3x，那么OG=5-3x，在Rt△DGO中，利用勾股定理可得（
）2=（4x）2+（
-3x）2，解得x1=
，x2=0（舍去），那么DG=
，则DF=
．
（2）在△ADG中SinA=
| 4 |
| 5 |
| DG |
| AD |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 5 |
| 12 |
| 5 |
| 24 |
| 5 |
解答：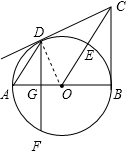
（1）证明：连接OD，
∵AD∥OC，
∴∠BOC=∠DAB，∠ADO=∠DOC，
又OA=OD，
∴∠DAB=∠ADO，
∴∠BOC=∠DAB=∠ADO=∠DOC，
在△ODC和△OBC中
，
∴△ODC≌△OBC，（SAS）
又∵BC⊥AB，
∴∠B=90°．
∴∠ODC=∠B=90°，
∴CD为⊙O的切线；
（2）解：在△ADG中，sinA=
=
，
设DG=4x，AD=5x，
∵DF⊥AB，∴G为DF的中点，
∴AG=3x，
又⊙O的半径为
，
∴OG=
-3x，
∵OD2=DG2+OG2，
∴（
）2=（4x）2+（
-3x）2，
∴x=
，
∴DG=4x=
，
∴DF=2DG=2×
=
．
（1）证明：连接OD，∵AD∥OC，
∴∠BOC=∠DAB，∠ADO=∠DOC，
又OA=OD，
∴∠DAB=∠ADO，
∴∠BOC=∠DAB=∠ADO=∠DOC，
在△ODC和△OBC中
|
∴△ODC≌△OBC，（SAS）
又∵BC⊥AB，
∴∠B=90°．
∴∠ODC=∠B=90°，
∴CD为⊙O的切线；
（2）解：在△ADG中，sinA=
| 4 |
| 5 |
| DG |
| AD |
设DG=4x，AD=5x，
∵DF⊥AB，∴G为DF的中点，
∴AG=3x，
又⊙O的半径为
| 5 |
| 2 |
∴OG=
| 5 |
| 2 |
∵OD2=DG2+OG2，
∴（
| 5 |
| 2 |
| 5 |
| 2 |
∴x=
| 3 |
| 5 |
∴DG=4x=
| 12 |
| 5 |
∴DF=2DG=2×
| 12 |
| 5 |
| 24 |
| 5 |
点评：本题利用了等边对等角、平行线的性质、全等三角形的判定和性质、切线的判定、三角函数值、解一元二次方程、勾股定理．
练习册系列答案
相关题目
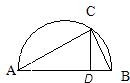9、如图AB为半圆的直径，C为半圆上的一点，CD⊥AB于D，连接AC，BC，则与∠ACD互余的角有（ ）
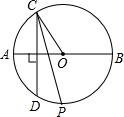如图AB为⊙O的直径，C为半圆AB上一点，过C作CD⊥AB交圆于点D，CP平分∠DOC，当C在半圆AB上运动时，则点P（ ）
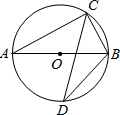如图AB为⊙O的直径，C、D是⊙O上两点，若∠ABC=55°，则∠D的度数为
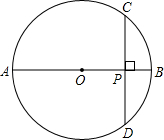如图AB为⊙O的直径，弦AB⊥CD，垂足为P，BP=2，CD=16，求直径AB的长．