题目内容
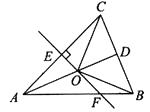
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
(1)判断AC与图中的那条线段相等,并证明你的结论;
(2)若CE的长为 ![]() ,求BG的长.
,求BG的长.
【答案】
(1)解:证明:∵CD⊥AB,
∴∠BDC=90°,
∵∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD,
∵BE⊥AC于E,
∴∠BEC=90°,
∵∠BFD=∠EFC,
∴∠DBF=∠DCA,
在Rt△DFB与Rt△DAC中,
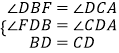 ,
,
∴Rt△DFB≌Rt△DAC,
∴BF=AC;
(2)解:∵BE平分∠ABC,

∴∠ABE=∠CBE=22.5°,
∵BE⊥AC于E,
∴∠BEA=∠BEC=90°,
又∵BE=BE,
∴Rt△BEA≌Rt△BEC,
∴CE=AE.
连结CG,
∵△BCD是等腰直角三角形,
∴BD=CD,
又H是BC边的中点,
∴DH⊥BC,
∴DH垂直平分BC,
∴BG=CG,
∵∠EBC=22.5°,
∴∠GCB=22.5°,
∴∠EGC=45°,
∴Rt△CEG是等腰直角三角形,
∵CE的长为 ![]() ,
,
∴EG= ![]() ,
,
利用勾股定理得:CE2+GE2=GC2,
∴ ![]() ,
,
∴ ![]() ,
,
∴BG的长为 ![]() .
.
【解析】(1)首先判断出△BCD是等腰直角三角形,根据等腰三角形的性质得出BD=CD,根据三角形的内角和得出∠DBF=∠DCA,然后利用AAS判断出Rt△DFB≌Rt△DAC,根据全等三角形的性质得出BF=AC;
(2)首先判断出Rt△BEA≌Rt△BEC,根据全等三角形对应边相等得出CE=AE.连结CG,根据等腰三角形的三线合一得出DH垂直平分BC,根据中垂线定理得出BG=CG,根据等边对等角得出∠EBC=22.5°=∠GCB,根据三角形的外角定理得出∠EGC=45°,故Rt△CEG是等腰直角三角形,利用勾股定理得出GC的长。
【考点精析】掌握线段垂直平分线的判定和线段垂直平分线的性质是解答本题的根本,需要知道和一条线段两个端点距离相等的点,在这条线段的垂直平分线上;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.