题目内容
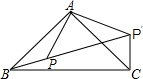 如图,△ABC是Rt△,BC是斜边,P是三角形内一点,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于
如图,△ABC是Rt△,BC是斜边,P是三角形内一点,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于3
| 2 |
3
.| 2 |
分析:根据旋转的性质得到AP′=AP=3,∠P′AP=∠CAB=90°,然后根据等腰直角三角形的性质可得到出PP′的长.
解答:解:∵△ABP绕点A逆时针旋转后,能与△ACP′重合,
∴AP′=AP=3,∠P′AP=∠CAB=90°,
∴△P′AP为等腰直角三角形,
∴P′P=
AP=3
.
故答案为3
.
∴AP′=AP=3,∠P′AP=∠CAB=90°,
∴△P′AP为等腰直角三角形,
∴P′P=
| 2 |
| 2 |
故答案为3
| 2 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目