题目内容
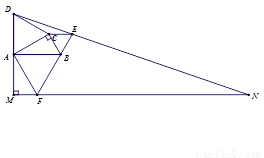
如图,△ABC是RT△,∠CAB=30°,BC=1,以AB、BC、AC为边分别作3个等边△ABF,△BCE,△ACD.过F作MF垂直DA的延长线于点M,连接并延长DE交MF的延长线于点N.那么△DMN的面积为

10
| 3 |
10
.| 3 |

分析:由△ABC是RT△,∠CAB=30°,BC=1,即可求得AB与AC的值,然后由以AB、BC、AC为边分别作3个等边△ABF,△BCE,△ACD,即可求得EF与DM的值,再过点E作EH⊥MN于H,即可求得FH与EH的值,继而求得梯形MHED的面积,再利用相似三角形的性质,即可求得△DMN的面积.
解答: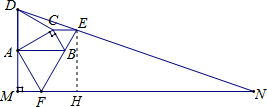 解:∵△ABC是RT△,∠CAB=30°,BC=1,
解:∵△ABC是RT△,∠CAB=30°,BC=1,
∴AB=2BC=2,AC=
=
=
,
∵△ABF,△BCE,△ACD是等边三角形,DM⊥MN,
∴FA=FB=AB=2,AD=AC=
,BE=BC=1,
∴∠DAB=∠DAC+∠CAB=90°,
∴∠MAF=∠MAB-∠FAB=90°-60°=30°,
∴∠AFM=60°,
∴AM=
,FM=1,
∴DM=AD+AM=2
,EF=BE+BF=3,
过点E作EH⊥MN于H,
∵∠AFM=∠AFB=60°,
∴∠EFH=180°-∠AFM-∠AFB=60°,
∴∠FEH=30°,
∴FH=
EF=
,EH=
,
∴MH=FM+FH=1+
=
,
∴S梯形MHED=
(EH+MD)•MH=
×(
+2
)×
=
,
∵DM⊥MN,EH⊥MN,
∴EH∥DM,
∴△EHN∽△DMN,
∴
=(
)2=(
)2=
,
∴S梯形MHED:S△DMN=7:16,
∴S△DMN=10
.
故答案为:10
.
 解:∵△ABC是RT△,∠CAB=30°,BC=1,
解:∵△ABC是RT△,∠CAB=30°,BC=1,∴AB=2BC=2,AC=
| BC |
| sin∠CAB |
| 1 | ||||
|
| 3 |
∵△ABF,△BCE,△ACD是等边三角形,DM⊥MN,
∴FA=FB=AB=2,AD=AC=
| 3 |
∴∠DAB=∠DAC+∠CAB=90°,
∴∠MAF=∠MAB-∠FAB=90°-60°=30°,
∴∠AFM=60°,
∴AM=
| 3 |
∴DM=AD+AM=2
| 3 |
过点E作EH⊥MN于H,
∵∠AFM=∠AFB=60°,
∴∠EFH=180°-∠AFM-∠AFB=60°,
∴∠FEH=30°,
∴FH=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴MH=FM+FH=1+
| 3 |
| 2 |
| 5 |
| 2 |
∴S梯形MHED=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 5 |
| 2 |
| 35 |
| 8 |
| 3 |
∵DM⊥MN,EH⊥MN,
∴EH∥DM,
∴△EHN∽△DMN,
∴
| S△EHN |
| S△DMN |
| EH |
| DM |
| ||||
2
|
| 9 |
| 16 |
∴S梯形MHED:S△DMN=7:16,
∴S△DMN=10
| 3 |
故答案为:10
| 3 |
点评:此题考查了相似三角形的判定与性质、含30°直角三角形的性质、等边三角形的性质等知识.此题难度较大,解题的关键是掌握含30°直角三角形的性质与相似三角形的面积比等于相似比的平方定理的应用,注意辅助线的作法.

练习册系列答案
相关题目
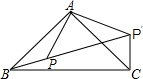 如图,△ABC是Rt△,BC是斜边,P是三角形内一点,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于
如图,△ABC是Rt△,BC是斜边,P是三角形内一点,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于