题目内容
【题目】如图①,在平面直角坐标系中,二次函数y=﹣ ![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.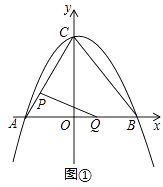
(1)填空:b= , c=;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
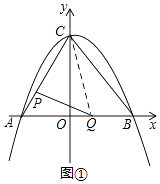
(4)如图②,点N的坐标为(﹣ ![]() ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
【答案】
(1)![]() ,4
,4
(2)解:在点P、Q运动过程中,△APQ不可能是直角三角形.
理由如下:连结QC.
∵在点P、Q运动过程中,∠PAQ、∠PQA始终为锐角,
∴当△APQ是直角三角形时,则∠APQ=90°.
将x=0代入抛物线的解析式得:y=4,
∴C(0,4).
∵AP=OQ=t,
∴PC=5﹣t,
∵在Rt△AOC中,依据勾股定理得:AC=5,在Rt△COQ中,依据勾股定理可知:CQ2=t2+16,在Rt△CPQ中依据勾股定理可知:PQ2=CQ2﹣CP2,在Rt△APQ中,AQ2﹣AP2=PQ2,
∴CQ2﹣CP2=AQ2﹣AP2,即(3+t)2﹣t2=t2+16﹣(5﹣t)2,解得:t=4.5.
∵由题意可知:0≤t≤4,
∴t=4.5不符合题意,即△APQ不可能是直角三角形.
(3)解:如图所示:
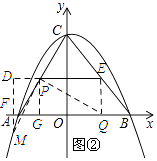
过点P作DE∥x轴,分别过点M、Q作MD⊥DE、QE⊥DE,垂足分别为D、E,MD交x轴与点F,过点P作PG⊥x轴,垂足为点G,则PG∥y轴,∠E=∠D=90°.
∵PG∥y轴,
∴△PAG∽△ACO,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
∴PG= ![]() t,AG=
t,AG= ![]() t,
t,
∴PE=GQ=GO+OQ=AO﹣AG+OQ=3﹣ ![]() t+t=3+
t+t=3+ ![]() t,DF=GP=
t,DF=GP= ![]() t.
t.
∵∠MPQ=90°,∠D=90°,
∴∠DMP+∠DPM=∠EPQ+∠DPM=90°,
∴∠DMP=∠EPQ.
又∵∠D=∠E,PM=PQ,
∴△MDP≌PEQ,
∴PD=EQ= ![]() t,MD=PE=3+
t,MD=PE=3+ ![]() t,
t,
∴FM=MD﹣DF=3+ ![]() t﹣
t﹣ ![]() t=3﹣
t=3﹣ ![]() t,OF=FG+GO=PD+OA﹣AG=3+
t,OF=FG+GO=PD+OA﹣AG=3+ ![]() t﹣
t﹣ ![]() t=3+
t=3+ ![]() t,
t,
∴M(﹣3﹣ ![]() t,﹣3+
t,﹣3+ ![]() t).
t).
∵点M在x轴下方的抛物线上,
∴﹣3+ ![]() t=﹣
t=﹣ ![]() ×(﹣3﹣
×(﹣3﹣ ![]() t)2+
t)2+ ![]() ×(﹣3﹣
×(﹣3﹣ ![]() t)+4,解得:t=
t)+4,解得:t= ![]() .
.
∵0≤t≤4,
∴t= ![]() .
.
(4)解:如图所示:连结OP,取OP的中点R,连结RH,NR,延长NR交线段BC与点Q′.
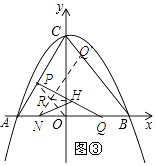
∵点H为PQ的中点,点R为OP的中点,
∴EH= ![]() QO=
QO= ![]() t,RH∥OQ.
t,RH∥OQ.
∵A(﹣3,0),N(﹣ ![]() ,0),
,0),
∴点N为OA的中点.
又∵R为OP的中点,
∴NR= ![]() AP=
AP= ![]() t,
t,
∴RH=NR,
∴∠RNH=∠RHN.
∵RH∥OQ,
∴∠RHN=∠HNO,
∴∠RNH=∠HNO,即NH是∠QNQ′的平分线.
设直线AC的解析式为y=mx+n,把点A(﹣3,0)、C(0,4)代入得: ![]() ,
,
解得:m= ![]() ,n=4,
,n=4,
∴直线AC的表示为y= ![]() x+4.
x+4.
同理可得直线BC的表达式为y=﹣x+4.
设直线NR的函数表达式为y= ![]() x+s,将点N的坐标代入得:
x+s,将点N的坐标代入得: ![]() ×(﹣
×(﹣ ![]() )+s=0,解得:s=2,
)+s=0,解得:s=2,
∴直线NR的表述表达式为y= ![]() x+2.
x+2.
将直线NR和直线BC的表达式联立得: 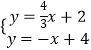 ,解得:x=
,解得:x= ![]() ,y=
,y= ![]() ,
,
∴Q′( ![]() ,
, ![]() ).
).
【解析】(1)设抛物线的解析式为y=a(x+3)(x﹣4).将a=﹣ ![]() 代入得:y=﹣
代入得:y=﹣ ![]() x2+
x2+ ![]() x+4,∴b=
x+4,∴b= ![]() ,c=4;(2)直角三角形存在性问题可采取假设的方法,然后根据三个内角哪一个可能为直角进行分类讨论;(3)由等腰直角三角形的性质可推得全等,用t 的代数式表示出M的坐标,根据在抛物线上代入解析式,建立方程求处t ,再验证它是否在取值范围内;(4) Q′可采用交轨法,即是直线NR和直线BC的交点,联立两个解析式组成方程组,解出方程组的解就是交点坐标.
,c=4;(2)直角三角形存在性问题可采取假设的方法,然后根据三个内角哪一个可能为直角进行分类讨论;(3)由等腰直角三角形的性质可推得全等,用t 的代数式表示出M的坐标,根据在抛物线上代入解析式,建立方程求处t ,再验证它是否在取值范围内;(4) Q′可采用交轨法,即是直线NR和直线BC的交点,联立两个解析式组成方程组,解出方程组的解就是交点坐标.

 全优点练单元计划系列答案
全优点练单元计划系列答案【题目】某商场甲、乙、丙三名业务员5个月的销售额(单位:万元)如下表:
月份 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 7.2 | 9.6 | 9.6 | 7.8 | 9.3 |
乙 | 5.8 | 9.7 | 9.8 | 5.8 | 9.9 |
丙 | 4 | 6.2 | 8.5 | 9.9 | 9.9 |
(1)根据上表中的数据,将下表补充完整:
统计值 | 平均数(万元) | 中位数(万元) | 众数(万元) |
甲 | 9.3 | 9.6 | |
乙 | 8.2 | 5.8 | |
丙 | 7.7 | 8.5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.