题目内容
【题目】通常情况下,用两种不同的方法计算同一图形的面积,可以得到一个恒等式,
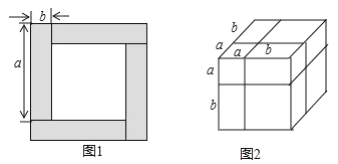
①如图1,根据图中阴影部分的面积可表示为__________,还可表示为___________,可以得到的恒等式是___________.
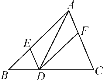
②类似地,用两种不同的方法计算同一各几何体的体积,也可以得到一个恒等式,如图2是边长为![]() 的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
的正方体,被如图所示的分割线分成8块。用不同方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式是____________.
【答案】①(a+b)2-(a-b)2;4ab;(a+b)2-(a-b)2=4ab; ②(a+b)3=a3+3a2b+3ab2+b3.
【解析】
①根据面积的不同求解方法,可得到不同的表示方法.一种是用大正方形面积-空白部分正方形面积;另一种是将阴影部分的四个长方形面积相加,可得等式(a+b)2-(a-b)2=4ab;
②根据体积的不同求解方法,可得到不同的表示方法.一种是将大正方体棱长表示出来求体积;另一种是将各个小的长方体体积加起来,可得等式(a+b)3=a3+3a2b+3ab2+b3.
解:①∵阴影部分的面积=大正方形的面积-中间小正方形的面积即:(a+b)2-(a-b)2,
又∵阴影部分的面积由4个长为a,宽为b的小正方形构成 即:4ab,
∴(a+b)2-(a-b)2=4ab;
故答案为:(a+b)2-(a-b)2;4ab;(a+b)2-(a-b)2=4ab;
②∵八个小正方体和长方体的体积之和是:a3+a2b+a2b+ab2+a2b+ab2+ab2+b3,
∴(a+b)3=a3+a2b+a2b+ab2+a2b+ab2+ab2+b3,
∴(a+b)3=a3+3a2b+3ab2+b3;
故答案为:(a+b)3=a3+3a2b+3ab2+b3.

【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t= ![]() ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A.1
B.2
C.3
D.4