题目内容
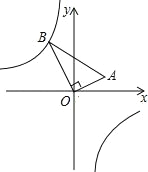
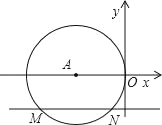
【题目】如图已知![]() 为⊙
为⊙![]() 的直径,
的直径,![]() 切⊙
切⊙![]() 于
于![]() 点,弦
点,弦![]() 于
于![]() 点,连结
点,连结![]() .
.
(1)探索![]() 满足什么条件时,有
满足什么条件时,有![]() ,并加以证明.
,并加以证明.
(2)当![]() ,
,![]() ,
,![]() ,求△
,求△![]() 面积.
面积.

【答案】(1)当AC平分∠BAD时,有AD⊥CD,理由见解析;(2)△OCF面积为12cm2
【解析】
(1)连接OC,由等边对等角得到∠OCA =∠OAC.再由角平分线定义得到∠OAC =∠DAC,等量代换得到∠OCA = ∠DAC ,根据内错角相等,两直线平行,得到 OC∥AD.由切线的性质及平行线的性质即可得出结论;
(2)先证明AC平分∠BAD,再根据角平分线的性质得到CD =CE,由垂径定理得到CF的长.在Rt△OEC中,由勾股定理得到OE的长,根据三角形的面积公式即可得出结论.
(1)当AC平分∠BAD时,有AD⊥CD.证明如下:
连接OC.
∵ OA = OC,∴ ∠OCA =∠OAC.
∵AC平分∠BAD,∴ ∠OAC =∠DAC,∴ ∠OCA = ∠DAC ,∴ OC∥AD.
∵ CD切⊙O于C点,∴ OC⊥CD,∴∠OCD=90°.
∵OC∥AD,∴∠ADC=180°-∠OCD=90°,∴AD⊥CD.
(2) 连接OF.
∵ CD切⊙O于C点,∴ OC⊥CD.
∵ AD⊥CD,∴ OC∥AD,∴∠OCA=∠DAC
∵ OA = OC,∴ ∠OCA =∠OAC,∴∠OAC =∠DAC,∴ AC平分∠BAD,∴ CD =CE.
∵ OA =5,CD =4,∴OC=OA=5,CE=4.
∵CF⊥AB ,∴CF = 2CE= 2×4=8,OE=![]() =
=![]() =3.
=3.
△OCF面积=CF×OE÷2= 8×3÷2=12.
故△OCF面积为12cm2.

练习册系列答案
相关题目