题目内容
【题目】如图,已知在Rt△ABC中,∠C=900,AD是∠BAC的角分线.
(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论;
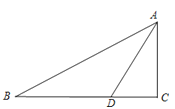
【答案】(1)作图见解析;(2)相切;证明见解析.
【解析】试题分析(1)因为AD是弦,所以圆心O即在AB上,也在AD的垂直平分线上;
(2)因为D在圆上,所以只要能证明OD⊥BC就说明BC为⊙O的切线.
试题解析:(1)如图所示,
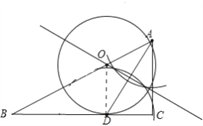
(2)相切;理由如下:
证明:连结OD,
∵OA=OD,
∴∠OAD=∠ODA
∵AD是BAC的角平分线,则∠OAD=∠DAC,
∴∠ODA=∠DAC,
∵AC⊥BC,则∠DAC+∠ADC=90°,
∴∠ODA+∠ADC=90°,即∠ODC=90°,
∴OD⊥BC,
即BC是⊙O的切线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目