��Ŀ����
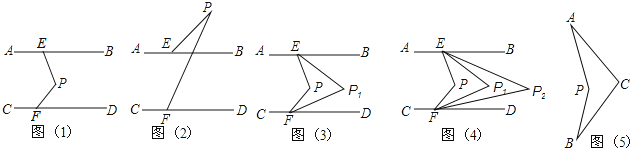
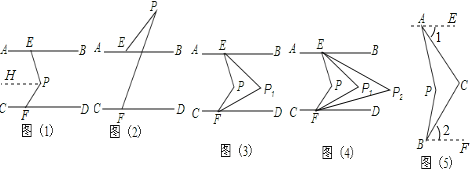
����Ŀ����ͼ��1����ֱ��AB��CD����P����ƽ����֮�䣬��E��AB�ϣ���F��CD�ϣ�����PE��PF��
��1����PEB����PFD����EPF�����������ϵ�� ����˵�����ɣ�
��2����ͼ��2��������P��ֱ��AB�ϲ�ʱ����PEB����PFD����EPF�����������ϵ�� ������˵�����ɣ�
��3����ͼ��3������ͼ��1�������ϣ�P![]() Eƽ�֡�PEB��P
Eƽ�֡�PEB��P![]() Fƽ�֡�PFD�������PEB=x�㣬��PFD=y�㣮���P
Fƽ�֡�PFD�������PEB=x�㣬��PFD=y�㣮���P![]() =______����x��y�Ĵ���ʽ��ʾ������P
=______����x��y�Ĵ���ʽ��ʾ������P![]() Eƽ�֡�P
Eƽ�֡�P![]() EB��P
EB��P![]() Fƽ�֡�P
Fƽ�֡�P![]() FD���ɵá�P
FD���ɵá�P![]() ��P
��P![]() Eƽ�֡�P
Eƽ�֡�P![]() EB��P
EB��P![]() Fƽ�֡�P
Fƽ�֡�P![]() FD���ɵá�P
FD���ɵá�P![]() ��������ƽ����ȥ�����P
��������ƽ����ȥ�����P![]() =______��
=______��
��4���Ƽ�����ϣ�����ͬѧ������һ��ͼ��5���ġ������ڡ������������֡�PAC=28�㣬
��PBC=30�㣬������֪����APB���ACB��������ϵ�����ܸ�������˵�����ɣ�
���𰸡���1����PEB����PFD����P�����������ϵ�ǡ�P=��PEB+��PFD�����ɼ�������
��2����PFD=��PEB+��P
��3����P1=![]() ����Pn=
����Pn=![]()
��4����APB=��C+58��
�������������������1������P��PH��AB��CD������ƽ���ߵ����ʣ���ֱ��ƽ�У��ڴ�����ȼ���֤�ã�
��2������P��ֱ��AB��ʱ����P��AB��ƽ���ߣ�ͬ��������ֱ��ƽ�У��ڴ�����ȼ���֤�ã�
��3�����ã�1���Ľ��ۺͽ�ƽ���ߵ����ʼ���д�����ۣ�
��4����A��B�ֱ���ֱ��AE��BF��ʹAE��BF�����ã�1���Ľ��ۼ�����⣮
���������(1)��PEB����PFD����P�����������ϵ�ǡ�P=��PEB+��PFD
�������£�����P��PH��AB��CD
���PEB=��EPH����PFD=��FPH
����EPF=��EPH+��FPH
���EPF=��PEB+��PFD
(2)��ͼ(2)������P��ֱ��AB��ʱ��
��PEB����PFD����P�����������ϵ�ǡ�PFD=��PEB+��P
(����˵������)
(3)��P1=![]() (x+y)��(��x,y�Ĵ���ʽ��ʾ)
(x+y)��(��x,y�Ĵ���ʽ��ʾ)
��Pn=(![]() )n(x+y)��.
)n(x+y)��.
(4)��APB=��C+58.�������£�
��A.B�ֱ���ֱ��AE��BF,ʹAE��BF.
��ͼ,��(1)���ɿ�֪��C=��1+��2.
��APB=��PAE+��PBF=(��PAC+��1)+(��PBC+��2)=��PAC+��PBC+(��1+��2)=��C+58��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�