题目内容
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG= ,则△CEF的面积是( )
,则△CEF的面积是( )
A. | B. | C. | D. |
A.
解析试题分析:∵AE平分∠BAD,
∴∠DAE=∠BAE;
又∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BEA=∠DAE=∠BAE,
∴AB=BE=6,
∵BG⊥AE,垂足为G,
∴AE=2AG.
在Rt△ABG中,∵∠AGB=90°,AB=6,BG= ,
,
∴AG= ,
,
∴AE=2AG=4;
∴S△ABE=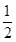 AE•BG=
AE•BG=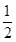 ×4×4
×4×4 =8
=8 .
.
∵BE=6,BC=AD=9,
∴CE=BC-BE=9-6=3,
∴BE:CE=6:3=2:1.
∵AB∥FC,
∴△ABE∽△FCE,
∴S△ABE:S△CEF=(BE:CE)2=4:1,
则S△CEF=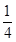 S△ABE=
S△ABE= .
.
故选A.
考点: 1.相似三角形的判定与性质;2.平行四边形的性质.

练习册系列答案
相关题目
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 ,那么点B′的坐标是
,那么点B′的坐标是
| A.(-2,3) | B.(2,-3) | C.(3,-2)或(-2,3) | D.(-2,3)或(2,-3) |
若 ,相似比为1:2,则
,相似比为1:2,则 与
与 的面积的比为( )
的面积的比为( )
| A.1:2 | B.2:1 | C.1:4 | D.4:1 |
如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形( )
| A.1对 | B.2对 | C.3对 | D.4对 |
两个相似多边形的面积比是9∶16,其中小多边形的周长为36 cm,则较大多边形的周长为 )
| A.48 cm | B.54 cm | C.56 cm | D.64 cm |
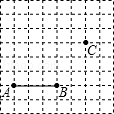

 ,则△CEF的面积是( )
,则△CEF的面积是( )


