题目内容
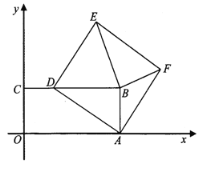
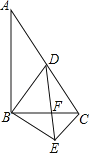
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 的中点,连接
的中点,连接![]() ,点
,点![]() 是
是![]() 边上的动点(不与点
边上的动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 延长线交于点
延长线交于点![]() ,连接
,连接![]() ,下列结论:
,下列结论:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③![]() 和
和![]() 一定相似;
一定相似;
④若![]() ,则
,则![]() .
.
其中正确的是_____.(填写所有正确结论的序号)
【答案】①②④
【解析】
①由直角三角形斜边上的中线等于斜边的一半,得AD=BD,由BF=CF,BD=CD得DE是BC的垂直平分线,得BE=CE,再由勾股定理便可得结论,由此判断结论的正误;②证明△ABC∽△DBE,求得BE,再证明DE∥AB,得DE垂直平分BC,得CE=BE,便可判断结论的正误;③证明∠ABD=∠CBE,再证明BE与BC或BC与BE两边的比不一定等于AB与BD的比,便可判断结论正误;④先求出AC,进而得BD,再在Rt△BCE中,求得BE,进而由勾股定理求得结果,便可判断正误.
解:①![]() 为斜边
为斜边![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
故①正确;
②![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即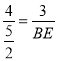 .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 垂直平分
垂直平分![]() ,
,
![]() ,
,
![]() ,
,
故②正确;
③![]() ,
,
![]() ,
,
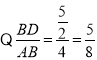 ,
,
但随着![]() 点运动,
点运动,![]() 的长度会改变,而
的长度会改变,而 ![]()
![]() 或
或![]() 不一定等于
不一定等于![]() ,
,
![]() 和
和![]() 不一定相似,
不一定相似,
故③错误;
④![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
故④正确;
故答案为:①②④.

练习册系列答案
相关题目