题目内容
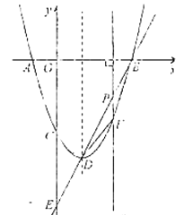
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 边上从点
边上从点![]() 运动到点
运动到点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,连
,连![]() ,在点
,在点![]() 运动过程中,请探究以下问题:
运动过程中,请探究以下问题:
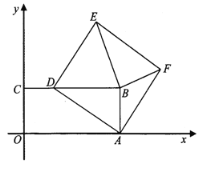
(1)![]() 的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
(2)若![]() 为等腰三角形,求此时正方形
为等腰三角形,求此时正方形![]() 的边长.
的边长.
【答案】(1)不变,![]() ;(2)正方形ADEF的边长为
;(2)正方形ADEF的边长为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)作![]() 交
交![]() 延长线于
延长线于![]() ,证明
,证明![]() ,从而可得
,从而可得 ![]() ,继而根据三角形面积公式进行计算即可;
,继而根据三角形面积公式进行计算即可;
(2)分![]() 、
、![]() 、
、![]() 三种情况分别讨论求解即可.
三种情况分别讨论求解即可.
(1)作![]() 交
交![]() 延长线于
延长线于![]() ,
,
∵正方形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵矩形![]() 中,
中,![]() ,
,![]()
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
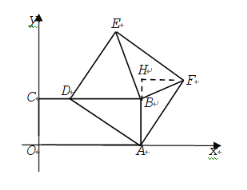
(2)①当![]() 时,作
时,作![]() ,
,
∵正方形![]() 中,
中,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
同(1)可得![]() ≌
≌![]() ,
,
∴![]() , ∴
, ∴![]() ,
,
∴![]() ;
;
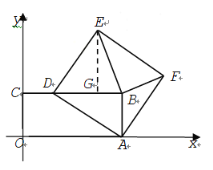
②当![]() 时,
时,![]() ,
,
∵正方形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵矩形![]() 中,
中,![]() ,
,
∴ ![]() ;
;

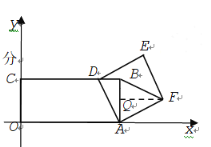
③当![]() 时,作
时,作![]() ,
,
同理得![]() ,
, ![]() ,
,
∴![]() ;
;
综上,正方形ADEF的边长为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目