题目内容
【题目】如图,在平面直角坐标系中,抛物线![]() 经过点A(﹣3,0)和点B(2,0).直线
经过点A(﹣3,0)和点B(2,0).直线![]() (
(![]() 为常数,且
为常数,且![]() )与BC交于点D,与
)与BC交于点D,与![]() 轴交于点E,与AC交于点F.
轴交于点E,与AC交于点F.
(1)求抛物线的解析式;
(2)连接AE,求![]() 为何值时,△AEF的面积最大;
为何值时,△AEF的面积最大;
(3)已知一定点M(﹣2,0).问:是否存在这样的直线![]() ,使△BDM是等腰三角形?若存在,请求出
,使△BDM是等腰三角形?若存在,请求出![]() 的值和点D的坐标;若不存在,请说明理由.
的值和点D的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在, ![]() ,D(
,D(![]() ,
,![]() ).
).
【解析】试题分析:(1)利用待定系数法即可解决问题.
(2)由题意可得点E的坐标为(0,h),点F的坐标为( ![]() ,h),根据S△AEF=
,h),根据S△AEF=![]() OEFE=
OEFE=![]() h
h![]() =-
=-![]() (h-3)2+
(h-3)2+![]() .利用二次函数的性质即可解决问题.
.利用二次函数的性质即可解决问题.
(3)分三种情形,分别列出方程即可解决问题.
试题解析:(1)将A(-3,0),点B(2,0)两点代入抛物线方程![]() 得,
得,
![]()
解得![]() ,
,
所以抛物线的解析式为![]() .
.
(2)如图所示,根据抛物线方程可知点C(0,6),
又∵A(-3,0)
∴直线AC的解析式为![]() ,
,
∵点F的纵坐标为![]() ,所以其横坐标为
,所以其横坐标为![]() ,即F(
,即F(![]() ,
,![]() )可得EF=
)可得EF=![]() ,
,
∴![]()
∴当![]() =3时,△AEF的最大面积为
=3时,△AEF的最大面积为![]() .
.
(3)∵B(2,0), C(0,6)
∴直线BC的解析式为![]() ,
,
∵点D的纵坐标为![]() ,所以其横坐标为
,所以其横坐标为![]() ,即D(
,即D(![]() ,
,![]() )
)
分三种情况讨论:
①当MD=BD时,点D应该在BM的垂直平分线y轴上,而![]() ﹤6∴点D不在y轴上,所以(舍)
﹤6∴点D不在y轴上,所以(舍)
②当MD=BM=4时,过D点做DQ⊥x轴于点Q, ∴MQ=![]() +2=4-
+2=4-![]() ,DQ=
,DQ= ![]()
在![]() 中
中![]() ∴
∴![]() 解得
解得![]() =0(舍)或
=0(舍)或![]() =
=![]()
∴D(![]() ,
,![]() )
)
③当BD=BM=4时,过D点做DQ⊥x轴于点Q, ∴BQ=2-![]() =
=![]() ,DQ=
,DQ= ![]()
在![]() 中
中![]() ∴
∴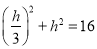 ,解得
,解得![]()
∴D(![]() ,
,![]() )
)

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目




