题目内容
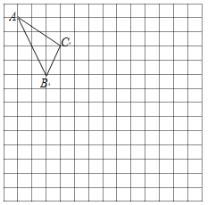
【题目】如图,在正方形网格中，每一个小正方形的边长为1．△ABC的三个顶点都在格点上，A、C的坐标分别是(﹣4，6)，(﹣1，4)．
(1)请在图中的网格平面内建立平面直角坐标系；
(2)请画出△ABC向右平移6个单位的△A1B1C1，并写出C1的坐标 ；
(3)请画出△ABC关于原点O对称的△A2B2C2 ， 并写出点C2的坐标 ．
【答案】(1)见解析；(2)见解析； (5,4) ；(3)见解析； (1,-4).
【解析】
（1）根据A、C两点的坐标建立平面直角坐标系即可；
（2）根据图形平移的性质画出△A1B1C1′，然后写出点C1坐标；
（3）分别作出点A、B、C关于原点O的对称点A2、B2、C2，连接A2、B2、C2即可得到△ABC关于原点O对称的△A2B2C2，然后写出点C2坐标．
解：(1)如图，建立平面直角坐标系；
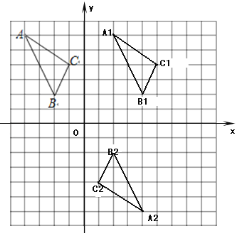
(2)如图，△A1B1C1为所作；点C1的坐标为(5,4) ；
(3)如图，△A2B2C2为所作；点C2的坐标为(1,-4).
故答案为：(1)见解析；(2)见解析； (5,4) ；(3)见解析； (1,-4).
练习册系列答案
相关题目
【题目】某中学形展“唱红歌”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示．
（1）根据图示填写下表：
班级 | 平均数（分） | 中位数（分） | 众数（分） |
九（1） | 85 | ||
九（2） | 85 | 100 |
（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；
（3）计算两班复赛成绩的方差．
