题目内容
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证: ![]() AC=BC+CD.
AC=BC+CD.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)利用条件易得∠ABD=∠ADB=45°,所以可知∠BAD=90°,∴△ABD为等腰直角三角形.
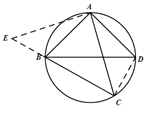
(2) 如图所示作CA⊥AE,延长CB交AE于点E,∠ACB=45°,CA⊥AE,△ACE为等腰直角三角形, ![]() AC=BC+EB,再证明△ABE和△ADC,EB=CD,
AC=BC+EB,再证明△ABE和△ADC,EB=CD, ![]() AC=BC+CD.
AC=BC+CD.
试题解析:
(1)∵弧AB=弧AB, ∴∠ADB=∠ACB,
又∵∠ACB=∠ABD=45°,∴∠ABD=∠ADB=45°,
∴∠BAD=90°,
∴△ABD为等腰直角三角形,
∴BD是该外接圆的直径.
(2)如图所示作CA⊥AE,延长CB交AE于点E
∵∠ACB=45°,CA⊥AE,∴△ACE为等腰直角三角形,
∴AC=AE,由勾股定理可知CE2=AC2+AE2=2AC2,
∴![]() ,由(1)可知△ABD 为等腰直角三角形,
,由(1)可知△ABD 为等腰直角三角形,
∴AB=AD,∠BAD=90°,又∵∠EAC=90°,
∴∠EAB+∠BAC=∠DAC+∠BAC,
∴∠EAB=∠DAC,
∴在△ABE和△ADC中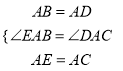 ,
,
∴△ABE≌△ADC(SAS),
∴BE=DC,
∴CE=BE+BC=DC+BC=![]() .
.

练习册系列答案
相关题目
