Question

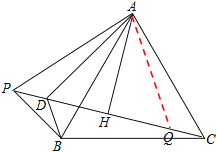
【题目】如图P为等边△ABC外一点，AH垂直平分PC于点H，∠BAP的平分线交PC于点D

(1) 求证：DP＝DB

(2) 求证：DA＋DB＝DC

(3) 若等边△ABC边长为，连接BH，当△BDH为等边三角形时，请直接写出CP的长度为_________

Answer 1

【答案】(1)证明见解析(2)证明见解析 (3)

【解析】试题分析：（1）首先由等边三角形的性质易得AB=AC=BC，由垂直平分线的性质易得AP=AC，即AP=AB，由SAS可证得△PAD≌△BAD，利用全等三角形的性质可得结论；

（2）在CP上截取CQ=PD，证明△ACQ≌△APD，利用全等三角形的性质可得△ADQ是等边三角形，得出结论；

（3）连接BH，延长AD交PB于点E，根据PA=PB，AD是角平分线得出AE⊥PB，且平分PB，由△BDH是等边三角形，知PD=BD，易得BD=DH=BH，∠BPH=30°，然后根据30°角的直角三角形的三角函数和勾股定理可求解.

试题解析：(1) ∵AH是PC的垂直平分线

∴PA＝PC＝AB

∵AD平分∠PAB

∴∠PAD＝∠BAD

在△PAD和△BAD中，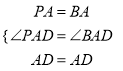

∴△PAD≌△BAD（SAS）

∴DP＝DB

(2) 在CP上截取CQ＝PD，连接AQ

∵AP＝AC

∴∠APD＝∠ACQ

在△APD和△ACQ中，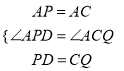

∴△APD≌△ACQ（SAS）

∴AD＝AQ，∠CAQ＝∠PAD

∴∠BAC＝∠CAQ＋∠BAQ＝∠PAD＋∠BAQ＝∠BAD＋∠BAQ＝∠DAQ＝60°

∴△ADQ为等边三角形

∴AD＝DQ

∴CD＝DQ＋CQ＝AD＋DB

(3) （提示：设DP＝DB＝DH＝x，则CH＝2x，CD＝3x，AD＝CD－DB＝2x）